流程引擎原理与实践

​ 实际上，工作流引擎的许多概念和机制都可以通过Petri网来描述和理解。例如，工作流引擎中的任务可以对应到Petri网中的变迁，工作流引擎中的工作流程可以对应到Petri网中的一系列转移和库所。通过Petri网，我们可以更好地理解和分析工作流引擎的行为，包括并发性、同步性、互斥性等。

# Petri网、工作流网与令牌机制

# Petri网基本概念、

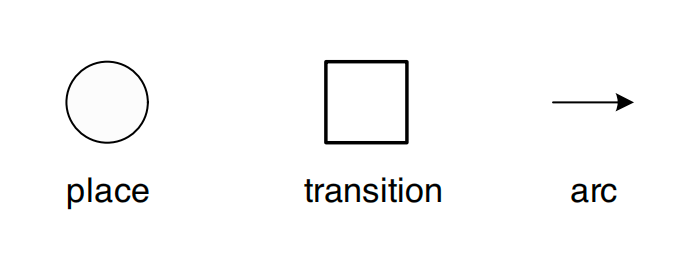
Petri网由库所（place）、变迁（transition）、有向弧（arc）和令牌（token）组成，形式上是一个有向双重图。

image-20240130232152375 image-20240313194427717

# 结构

Petri网的元素：

  • 库所（Place）圆形节点，表示系统的状态或资源，是一个被动的组件，可以存储令牌。

  • 变迁（Transition）方形节点，表示系统中可能发生的事件或动作，每个变迁都会导致令牌的转移。

  • 有向弧（Arc）是库所和变迁之间的有向弧，表示状态和事件之间的依赖关系。弧线上的数字代表要消耗的令牌数（为了避免混乱，当数字为1时默认不显示）。有向弧只允许库所指向变迁或者变迁指向库所。

    image-20240313200218975

  • 令牌（Token）是库所中的动态对象，可以从一个库所移动到另一个库所。

打个比方：token就像电流，transition就像设备，arc是电线，电流（token）根据电线（arc）经过设备（transition），设备就会有反应（例如：灯亮了、风扇动了等）

# 规则

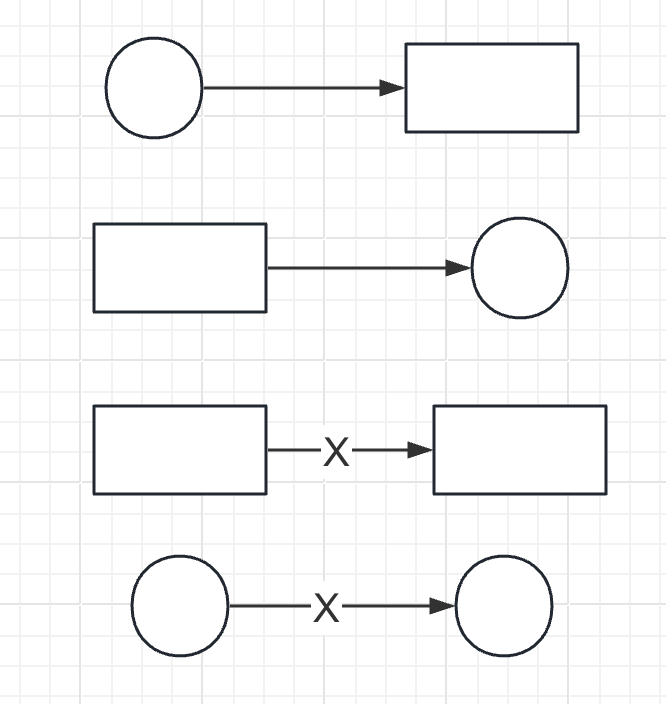
  • 有向弧是有方向的
  • 两个库所之间或两个变迁之间不允许有弧
  • 库所可以拥有任意数量的令牌

# 行为

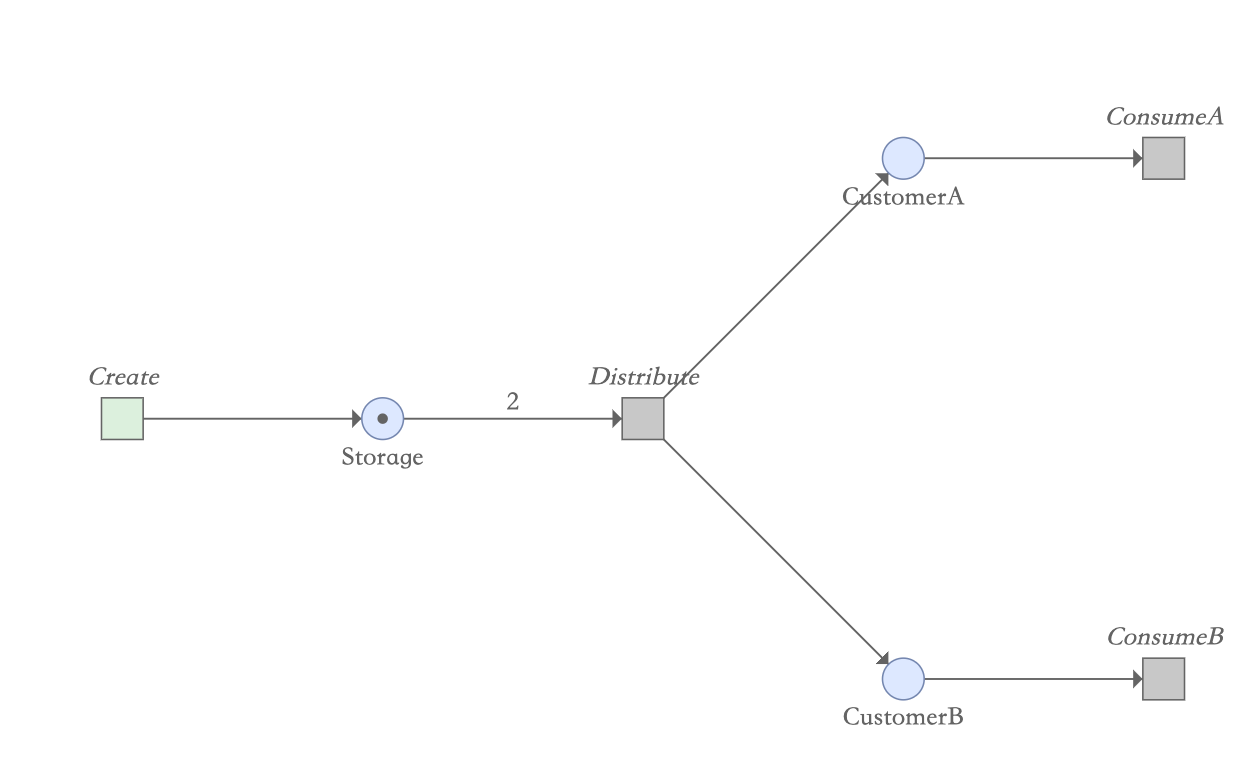
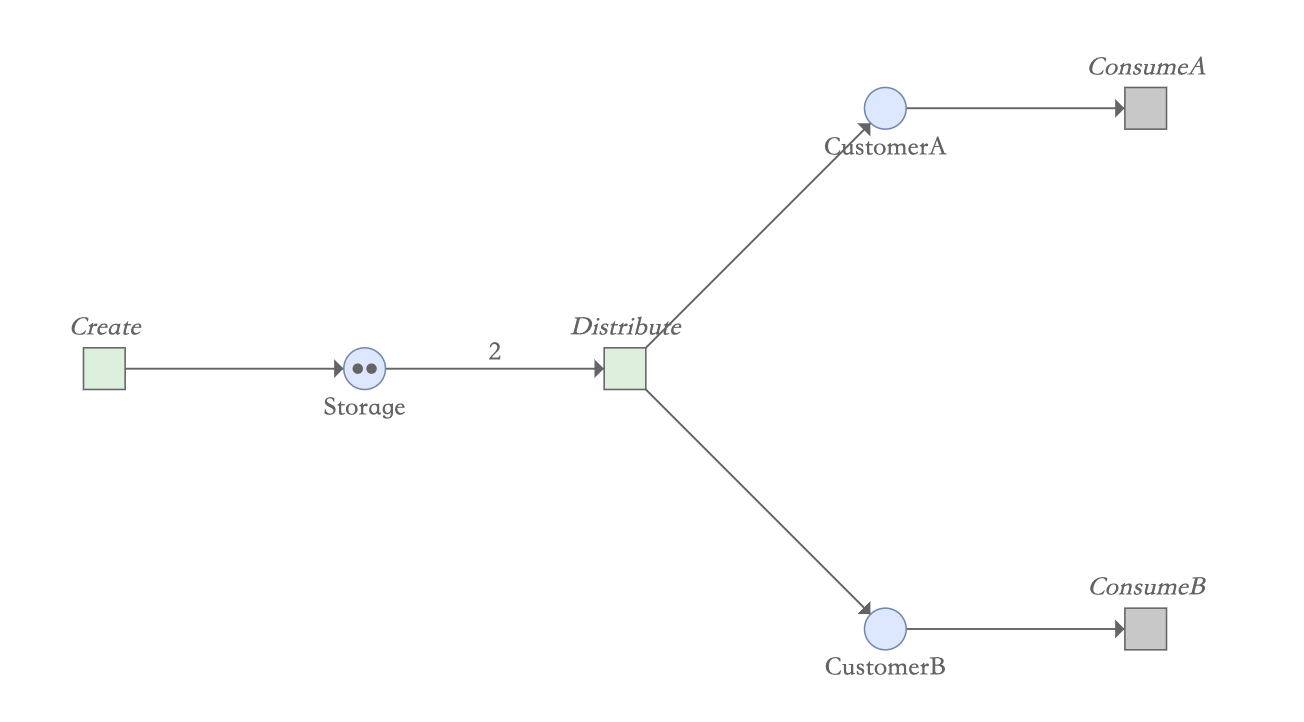
如果一个变迁的每个输入库所（input place）都拥有令牌时，该变迁即为被允许（enable）。一个变迁被允许时，变迁将发生（fire），输入库所（input place）的令牌被消耗，同时为输出库所（output place）产生令牌。

例如前面的例子：我们看到当库所Storage只有1个令牌时，变迁Distribute是没有被激活的。当库所Storage有2个令牌时，满足了变迁发生所需的令牌数，此时变迁Distribute被激活了。

image-20240313194514121

# 并发和汇聚 split-join

表达并行发生的事件通常是必要的。下图的网络展示了如何将单个顺序进程分为两个并行运行然后同步的分支。

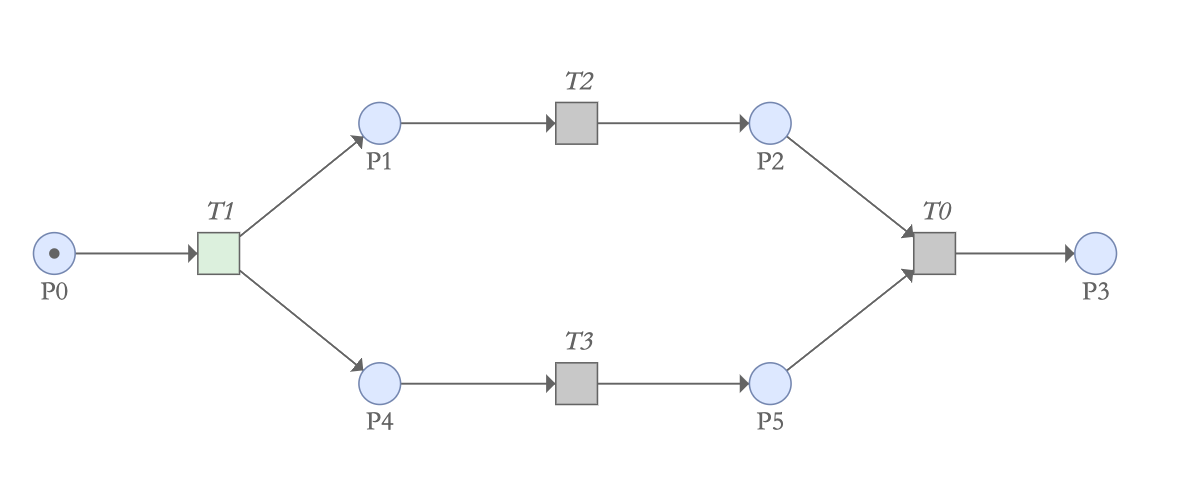
image-20240313195009633

当令牌通过变迁T1以后，会复制同样分支个数的令牌给库所P1和P4，

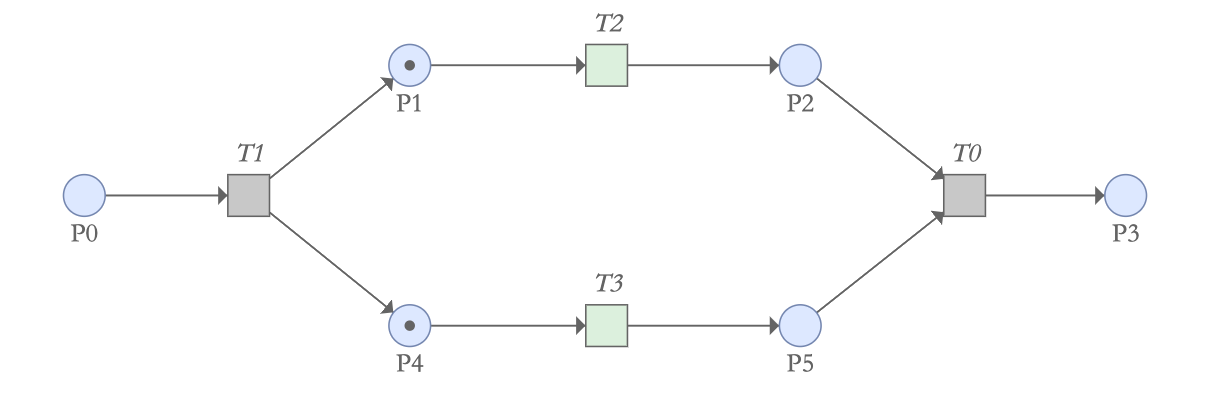
image-20240313195125379

并且只有当库所P2和P5都拥有令牌时，变迁T0才能被激活。

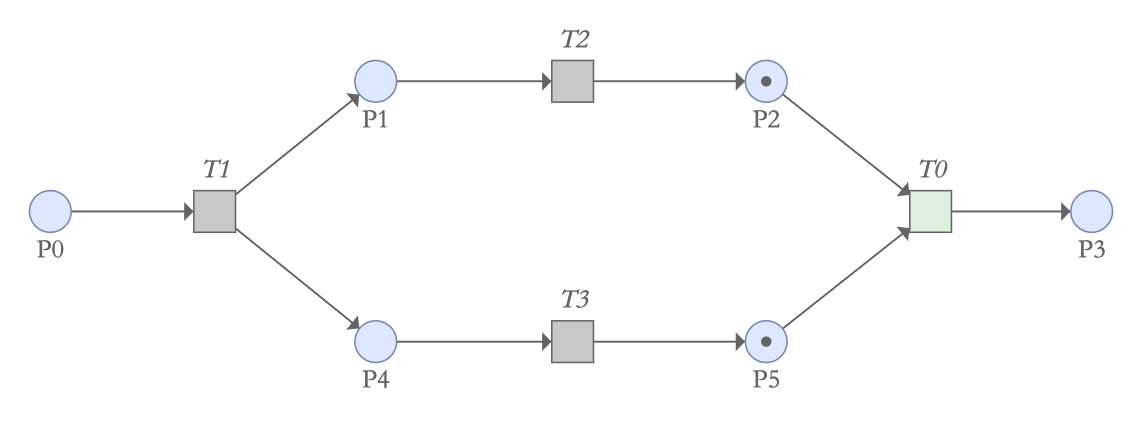
image-20240313195327580

两个令牌经过变迁T0后又被合并会一个令牌传递给P3。

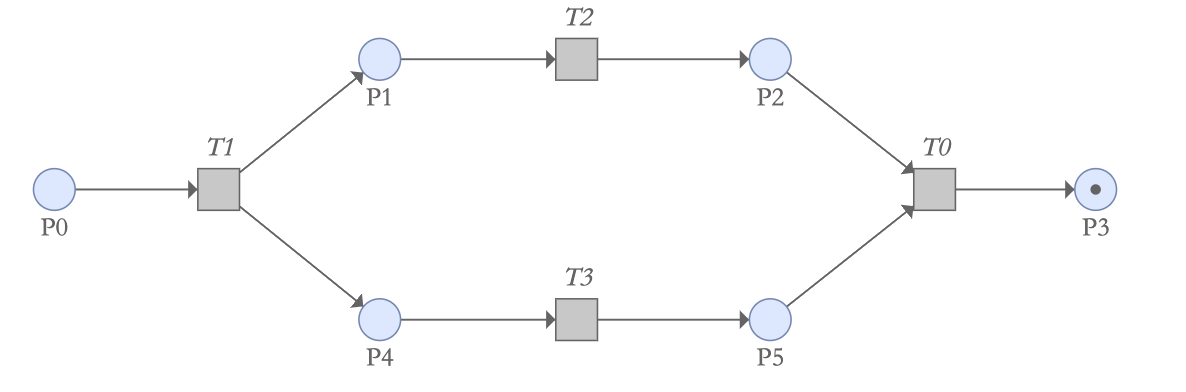
image-20240313195427084

# 例子

如下图，库所A开始时拥有2个令牌，可以看到这是变迁1是被允许发生的（绿色），而其他变迁2和3此时是不允许发生（灰色）。

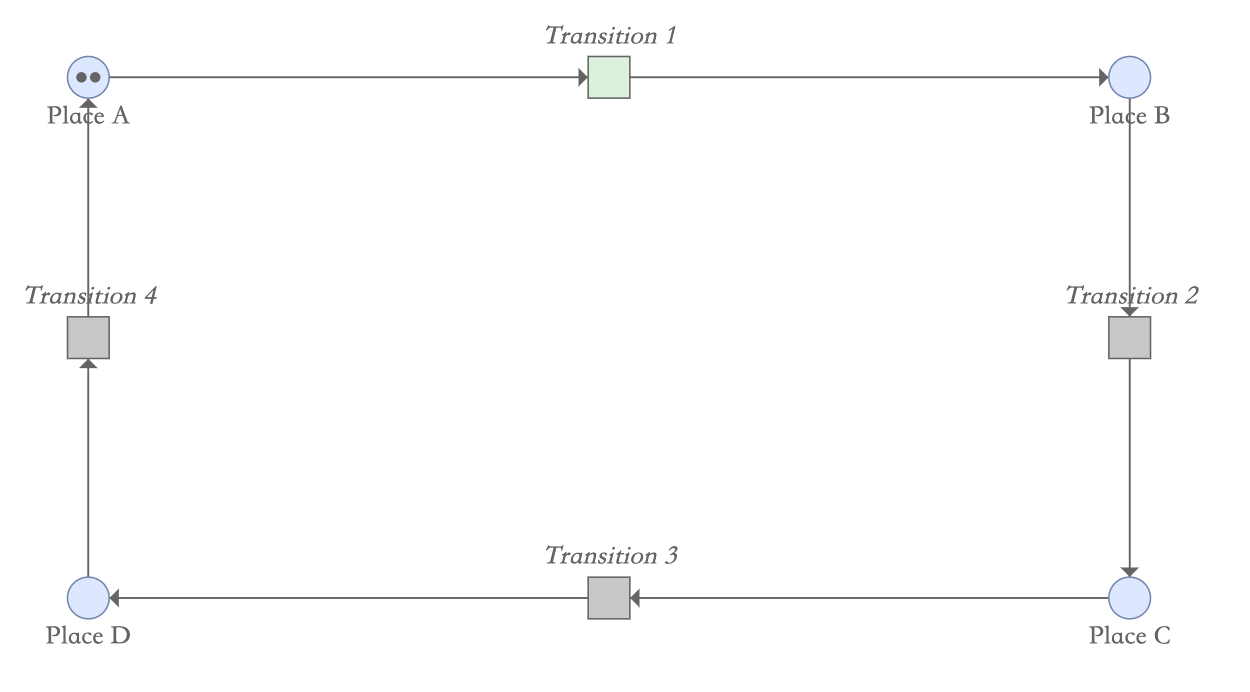
image-20240313193500111

当变迁1发生后，库所A的一个令牌会移动到库所B，此时变迁1和2都处于允许状态，因为他们的输入库所都拥有令牌。

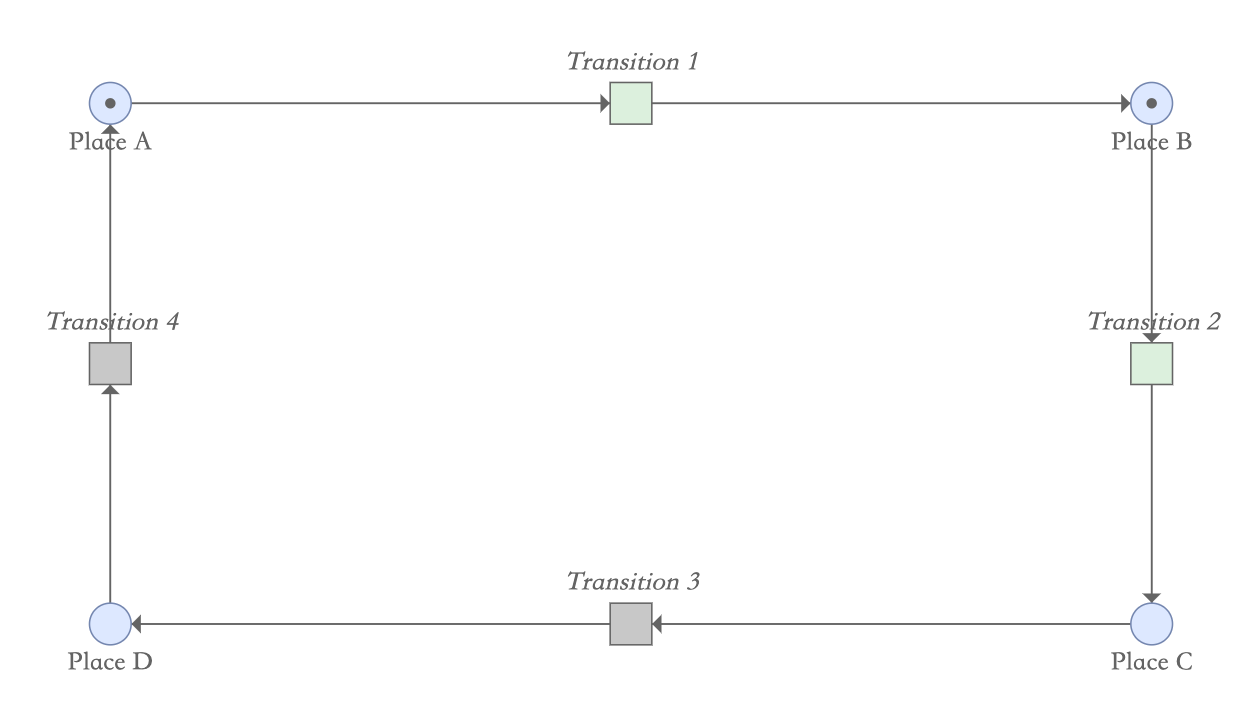
image-20240313193626571

当变迁2发生以后，库所B的令牌就移动到库所C，导致变迁3变成激活的，而变迁2由于输入库所B没有令牌，所以不被允许变迁。

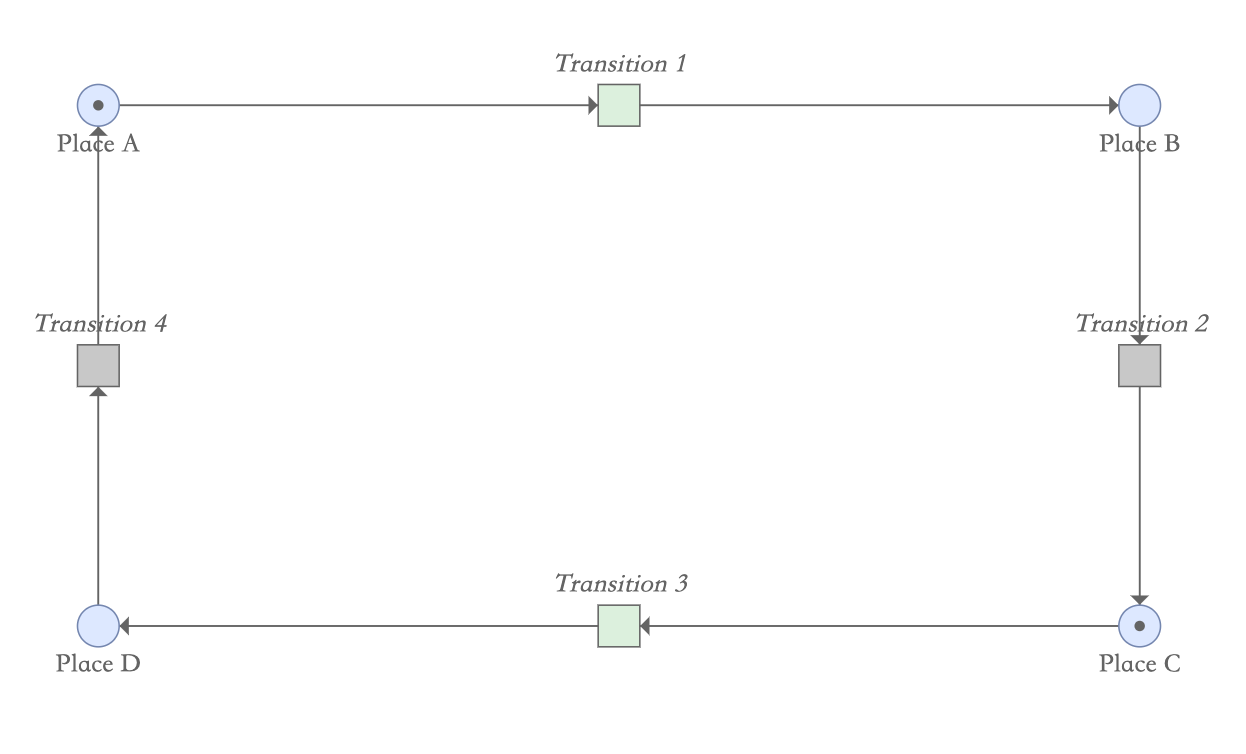
image-20240313193800321

接下来变迁3发生后，库所C的令牌移动到库所D，此时变迁4状态变成激活的，而变迁3无法发生。

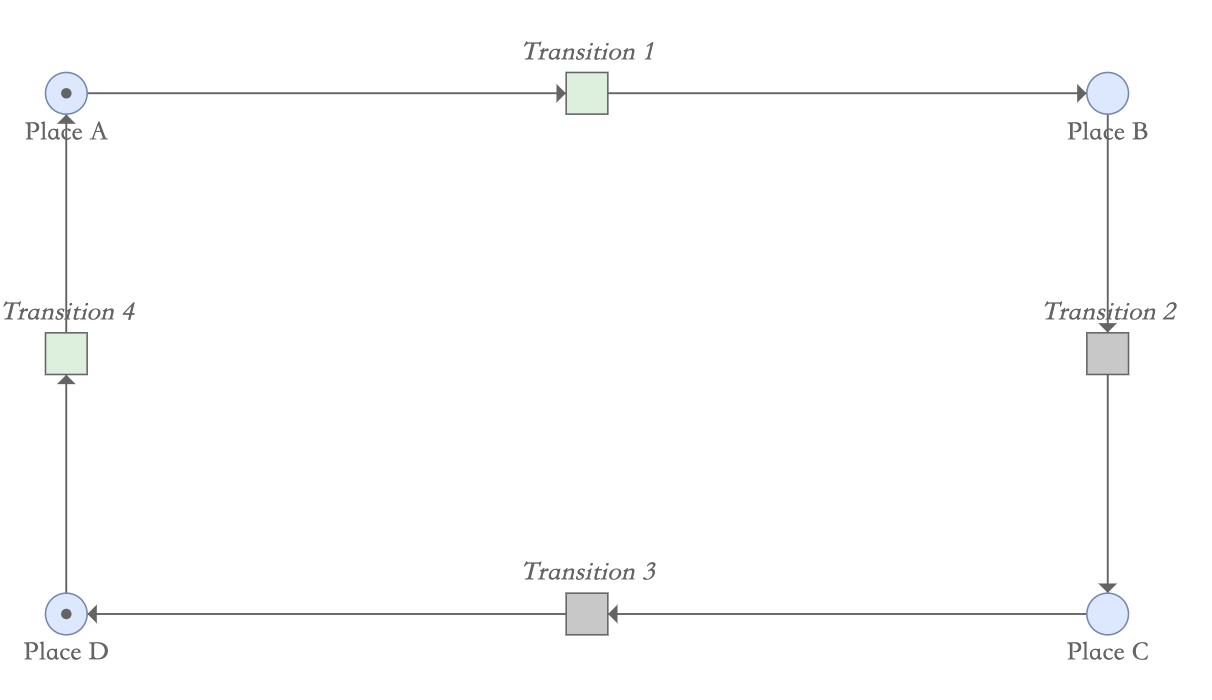
image-20240313193859485

最后，变迁4发生以后，令牌又回到库所A，变成只有变迁1是激活的。

image-20240313193500111

# 工作流网基本概念

工作流网（Workflow Net）是一种基于Petri网的建模方法，是一种特殊的Petri网，专门用于描述和分析工作流程系统。它是由荷兰计算机科学家Wil van der Aalst教授于1990年代提出的。工作流网在Petri网的基础上，增加了特定的约束和结构，使其更适合表示工作流程。

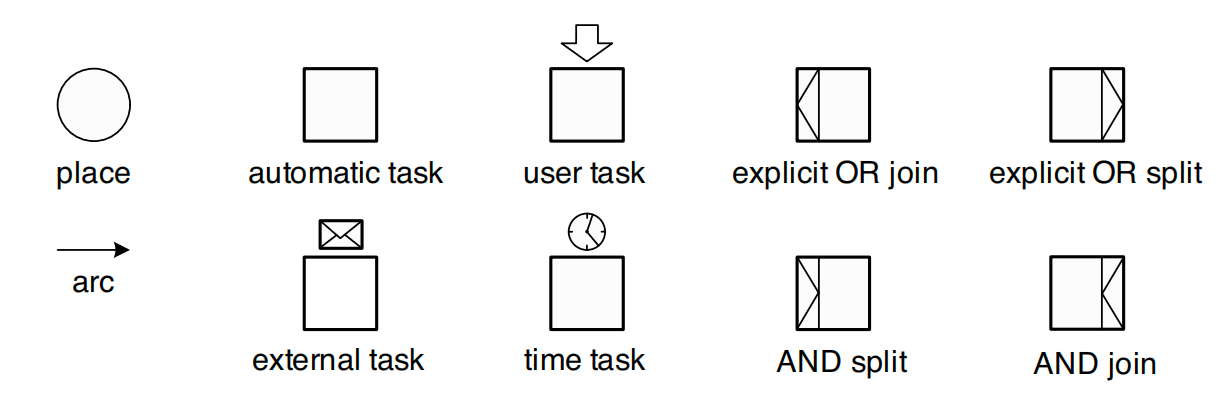
image-20240130232233617

主要包括以下特点：

  • 具有唯一的开始库所和结束库所，分别表示工作流程的开始和结束。同时，开始库所没有入边，结束库所没有出边。
  • 每个库所和变迁都在开始库所到结束库所的路径上，即不存在孤立的库所。
  • 变迁（transition）表示工作流程中的任务或活动。在这里的变迁类型做了更进一步的划分，如上图所示：除了自动化任务，还有人工任务、事件任务以及分支汇聚类型的任务。
  • 库所（place）表示工作流程中的状态或条件。
  • 有向弧表示任务之间的依赖关系和资源流动。

而一个合理的工作流网，需要同时满足以下几个条件：

  • 开始库所中的每个Token，最终都会在结束库所中产生一个Token。就是说明工作流网最终一定会结束，没有结束的工作流网是没有意义。
  • 当Token出现在结束库所时，其他库所都为空没有Token。
  • 在可达图中，每个变迁都能被使能。这保证每个路径都是有意义的。

可见，工作流网的特点更接近于我们的本书描述的流程。

# Petri网算法实现步骤

以下是实现Petri网算法的一般流程：

  1. 定义Petri网的数据结构，通常包括：
    • 库所（place）：表示系统的状态，可以包含令牌（token）。
    • 变迁（transition）：表示系统中可能发生的事件或操作，它连接输入库所和输出库所。
    • 弧（arc）：表示库所和变迁之间的关系，指示令牌如何在库所之间移动。
  2. 初始化Petri网，包括：
    • 添加库所，并为起始库所分配初始令牌。
    • 添加变迁，并定义每个变迁的输入库所、输出库所和关联的操作（可选）。
  3. 执行Petri网，通常包括以下步骤：
    • 确定当前可执行的变迁：检查所有变迁，确定哪些变迁具有足够的输入令牌来执行。
    • 选择一个可执行的变迁：根据某种策略（如优先级、随机选择等）选择一个可执行的变迁。
    • 执行所选的变迁：从输入库所中移除令牌，将令牌放入输出库所，并执行关联的操作（可选）。
    • 重复执行上述步骤，直到没有可执行的变迁或达到预定义的结束条件。
  4. 分析和验证Petri网的行为：根据实际需求，可以对Petri网的执行结果进行分析和验证，以确保它符合预期的行为。

这是一个通用的Petri网算法实现流程。在实际应用中，可能需要根据具体需求对这个流程进行扩展和优化。例如，可以添加更复杂的变迁类型（如带有优先级或抑制弧的变迁），或者实现更高级的分析和验证方法。

# Petri网令牌机制实践（单线程版本）

在Petri网中，系统的状态由令牌（token）的分布来表示，这些令牌在库所（place）之间按照一定的规则（transition）移动。

以下是一个简单的Python实现，定义了一个Petri网，以及一个函数来执行一个变迁。并且定义一个Transition类，这个类可以存储关联的输入和输出库所，以及一个可执行的函数。

在这个例子中，我们将创建一个Petri网，它包含多个变迁，以及一个自定义函数，用于在执行变迁时打印信息。

class PetriNet:
    def __init__(self):
        self.places = {}
        self.transitions = {}

    def add_place(self, name, tokens=0):
        self.places[name] = tokens

    def add_transition(self, name, transition):
        self.transitions[name] = transition

    def execute_transition(self, name):
        transition = self.transitions[name]
        if not transition.can_execute(self.places):
            print(f"Transition {name} cannot be executed due to lack of tokens")
            return
        transition.execute(self.places)
        print(f"Transition {name} executed successfully")


class Transition:
    def __init__(self, inputs, outputs, func=None):
        self.inputs = inputs
        self.outputs = outputs
        self.func = func

    def can_execute(self, places):
        for place, tokens in self.inputs.items():
            # 判断库所的输入令牌数是否足够
            if places.get(place, 0) < tokens:
                return False
        return True

    def execute(self, places):
        for place, tokens in self.inputs.items():
            places[place] -= tokens
        for place, tokens in self.outputs.items():
            places[place] += tokens
        if self.func:
            self.func()


def print_info(transition_name):
    print(f"Executing transition {transition_name}")

pn = PetriNet()

# 添加库所
pn.add_place("p1", tokens=2)
pn.add_place("p2")
pn.add_place("p3")

# 添加变迁
t1 = Transition({"p1": 1}, {"p2": 1}, lambda: print_info("t1"))
t2 = Transition({"p2": 1}, {"p3": 1}, lambda: print_info("t2"))

pn.add_transition("t1", t1)
pn.add_transition("t2", t2)

# 执行变迁
pn.execute_transition("t1")  # 输出：Executing transition t1
                             #       Transition t1 executed successfully

pn.execute_transition("t2")  # 输出：Executing transition t2
                             #       Transition t2 executed successfully

pn.execute_transition("t1")  # 输出：Executing transition t1
                             #       Transition t1 executed successfully
  
pn.execute_transition("t2")  # 输出：Executing transition t2
                             #       Transition t2 executed successfully

pn.execute_transition("t1")  # 输出：Transition t1 cannot be executed due to lack of tokens

在这个例子中，我们创建了一个包含3个库所（p1, p2, p3）和2个变迁（t1, t2）的Petri网。

初始时，库所p1有2个令牌。当执行变迁t1时，它会从p1中移除一个令牌，并将其放入p2。执行变迁t2时，它会从p2中移除一个令牌，并将其放入p3。我们还添加了一个自定义函数，用于在执行变迁时打印变迁的名称。在执行过程中，我们可以看到这些函数被正确地调用。最后，当再次尝试执行t1时，由于p1中没有足够的令牌，变迁将无法执行。

通过如下命令执行代码：

python petrinet.py

如果一切顺利，你可能会得到如下的输出：

Executing transition t1
Transition t1 executed successfully
Executing transition t2
Transition t2 executed successfully
Executing transition t1
Transition t1 executed successfully
Executing transition t2
Transition t2 executed successfully
Transition t1 cannot be executed due to lack of tokens

当然，前面还有一个问题，我们怎么判断这个流程结束了？

在Petri网中，流程是否结束通常取决于你的使用场景和定义。一种常见的方法是检查是否还有可以执行的变迁。如果没有任何变迁可以执行，我们可以认为流程已经结束。

我们可以在PetriNet类中添加一个方法来检查是否还有可执行的变迁：

class PetriNet:
    # ...其它方法...

    def has_executable_transitions(self):
        for transition in self.transitions.values():
            if transition.can_execute(self.places):
                return True
        return False

这个方法会检查每一个变迁，看它们是否可以在当前的令牌分布下执行。如果有任何一个变迁可以执行，它就会返回True。如果没有任何变迁可以执行，它就会返回False。

然后，在你的主程序中，你可以使用一个循环来持续执行变迁，直到没有可执行的变迁为止：

while pn.has_executable_transitions():
    # 在这里，你可以选择一个可以执行的变迁来执行
    # 这个选择可能是随机的，也可能是基于某种策略的
    # 在这个例子中，我们只是简单地执行第一个可以执行的变迁
    for name, transition in pn.transitions.items():
        if transition.can_execute(pn.places):
            pn.execute_transition(name)
            break

这个循环会持续执行，直到没有可执行的变迁为止，此时我们可以认为流程已经结束。

# Petri网令牌机制实践（多线程版本）

import time
import threading

class PetriNet:
    def __init__(self):
        self.places = {}
        self.transitions = {}

    def add_place(self, name, tokens=0):
        self.places[name] = tokens

    def add_transition(self, name, transition):
        self.transitions[name] = transition
        
    def has_executable_transitions(self):
        for transition in self.transitions.values():
            if transition.can_execute(self.places):
                return True
        return False

    def execute_transition(self, name):
        transition = self.transitions[name]
        if not transition.can_execute(self.places):
            print(f"Transition {name} cannot be executed due to lack of tokens")
            return
        transition.execute(self.places)
        print(f"Transition {name} executed successfully")
        
    def run(self):
        print(f"Init => {self.places}\n")
        while self.has_executable_transitions():
            for name, transition in self.transitions.items():
                if transition.can_execute(self.places):
                    self.execute_transition(name)
                    print(f"After transition=> {self.places}\n")
                    break
            time.sleep(0.1)  # 避免过度占用CPU资源
        


class Transition:
    def __init__(self, inputs, outputs, func=None):
        self.inputs = inputs
        self.outputs = outputs
        self.func = func

    def can_execute(self, places):
        for place, need_tokens in self.inputs.items():
            if places.get(place, 0) < need_tokens:
                return False
        return True

    def execute(self, places):
        for place, tokens in self.inputs.items():
            places[place] -= tokens
        for place, tokens in self.outputs.items():
            places[place] += tokens
        if self.func:
            self.func()

# 使用示例
def print_hello():
    print("Hello, world!")

def print_info(transition_name):
    print(f"Executing transition {transition_name}")


def main():
    pn = PetriNet()

    # 添加库所
    pn.add_place("p1", tokens=1)
    pn.add_place("p2")
    pn.add_place("p3")

    # 添加变迁
    # t1表示这个迁移要发生，则前置的place必须要有1个token。
    # 同理t2要发生迁移，前置的place也需要有1个token。
    t1 = Transition({"p1": 1}, {"p2": 1}, lambda: print_info("t1"))
    t2 = Transition({"p2": 1}, {"p3": 1}, lambda: print_info("t2"))

    pn.add_transition("t1", t1)
    pn.add_transition("t2", t2)

    # 创建并启动一个新线程来执行Petri网
    t = threading.Thread(target=pn.run)
    t.start()

    # 在主线程中检查Petri网是否已经结束
    while t.is_alive():
        print("Petri net is still running...")
        time.sleep(1)

    print("Petri net has finished.")
    

main()

main函数中创建的Petri网例子如下图所示：

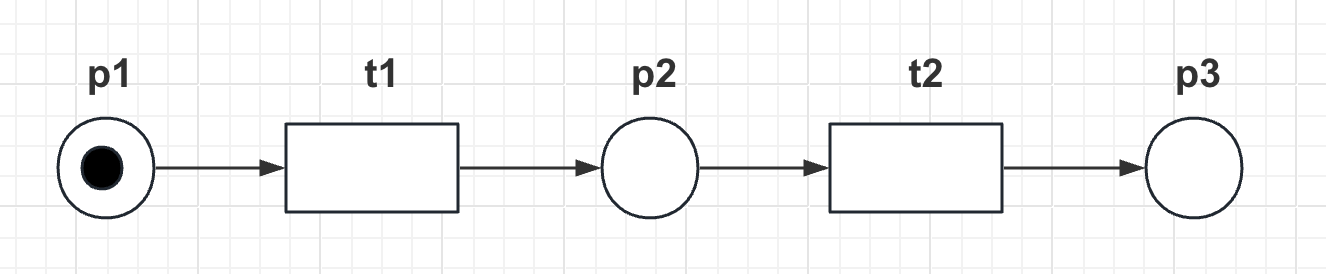
image-20240313125353884

执行命令：

python petrinet-thread.py

如一切顺利，你会得到如下输出：

Init => {'p1': 1, 'p2': 0, 'p3': 0}

Executing transition t1
Transition t1 executed successfully
After transition=> {'p1': 0, 'p2': 1, 'p3': 0}

Petri net is still running...
Executing transition t2
Transition t2 executed successfully
After transition=> {'p1': 0, 'p2': 0, 'p3': 1}

Petri net has finished.

如果我们把p1初始化的令牌改为0，再次运行上面的代码，会发现流程根本不运行，这是因为t1变迁的输入库所p1没有令牌。

AND Split并发路由

前面我们代码测试的Petri网都是顺序的，下面我们来测试前面带并发分支的情况：

image-20240313195009633

把前面的main函数改成如下的例子，下面的例子Petr网如上图所示。

# 其他代码...
def main():
		# 示例
    pn = PetriNet()
    pn.add_place("p0", tokens=1)
    pn.add_place("p1")
    pn.add_place("p2")
    pn.add_place("p3")
    pn.add_place("p4")
    pn.add_place("p5")

    # AND split
    t1 = Transition({"p0": 1}, {"p1": 1, "p4": 1})
    pn.add_transition("t1", t1)

    # p1 -> [t2] -> p2
    t2 = Transition({"p1": 1}, {"p2": 1})
    pn.add_transition("t2", t2)

    # p4 -> [t3] -> p5
    t3 = Transition({"p4": 1}, {"p5": 1})
    pn.add_transition("t3", t3)

    # AND join
    t0 = Transition({"p2": 1, "p5": 1}, {"p3": 1})
    pn.add_transition("t0", t0)

    # 创建并启动一个新线程来执行Petri网
    t = threading.Thread(target=pn.run)
    t.start()

    while t.is_alive():
        print("Petri net is still running...")
        time.sleep(1)

    print("Petri net has finished.")

执行如下命令：

python petrinet-thread.py

如一切顺利，会得到如下输出：

Init => {'p0': 1, 'p1': 0, 'p2': 0, 'p3': 0, 'p4': 0, 'p5': 0}

Petri net is still running...
Transition t1 executed successfully
After transition=> {'p0': 0, 'p1': 1, 'p2': 0, 'p3': 0, 'p4': 1, 'p5': 0}

Transition t2 executed successfully
After transition=> {'p0': 0, 'p1': 0, 'p2': 1, 'p3': 0, 'p4': 1, 'p5': 0}

Transition t3 executed successfully
After transition=> {'p0': 0, 'p1': 0, 'p2': 1, 'p3': 0, 'p4': 0, 'p5': 1}

Transition t0 executed successfully
After transition=> {'p0': 0, 'p1': 0, 'p2': 0, 'p3': 1, 'p4': 0, 'p5': 0}

Petri net has finished.
最后更新: 9/12/2024, 11:20:51 PM

← 4.2.6 开源YAWL Petri网调度算法剖析 →