资源调度机制介绍

我在引言章节中概括了流程引擎本质上是解决两个功能。前面内容介绍的任务调度算法（包括DAG、FSM和Petri网算法）是解决第一个问题，而第二个问题就是本章要介绍的资源调度机制。这两个功能是引擎的核心，特别是资源调度机制，这个更是系统实现降本增效的关键。

（1）以什么样的顺序执行任务

（2）决定由谁（资源）执行哪个任务

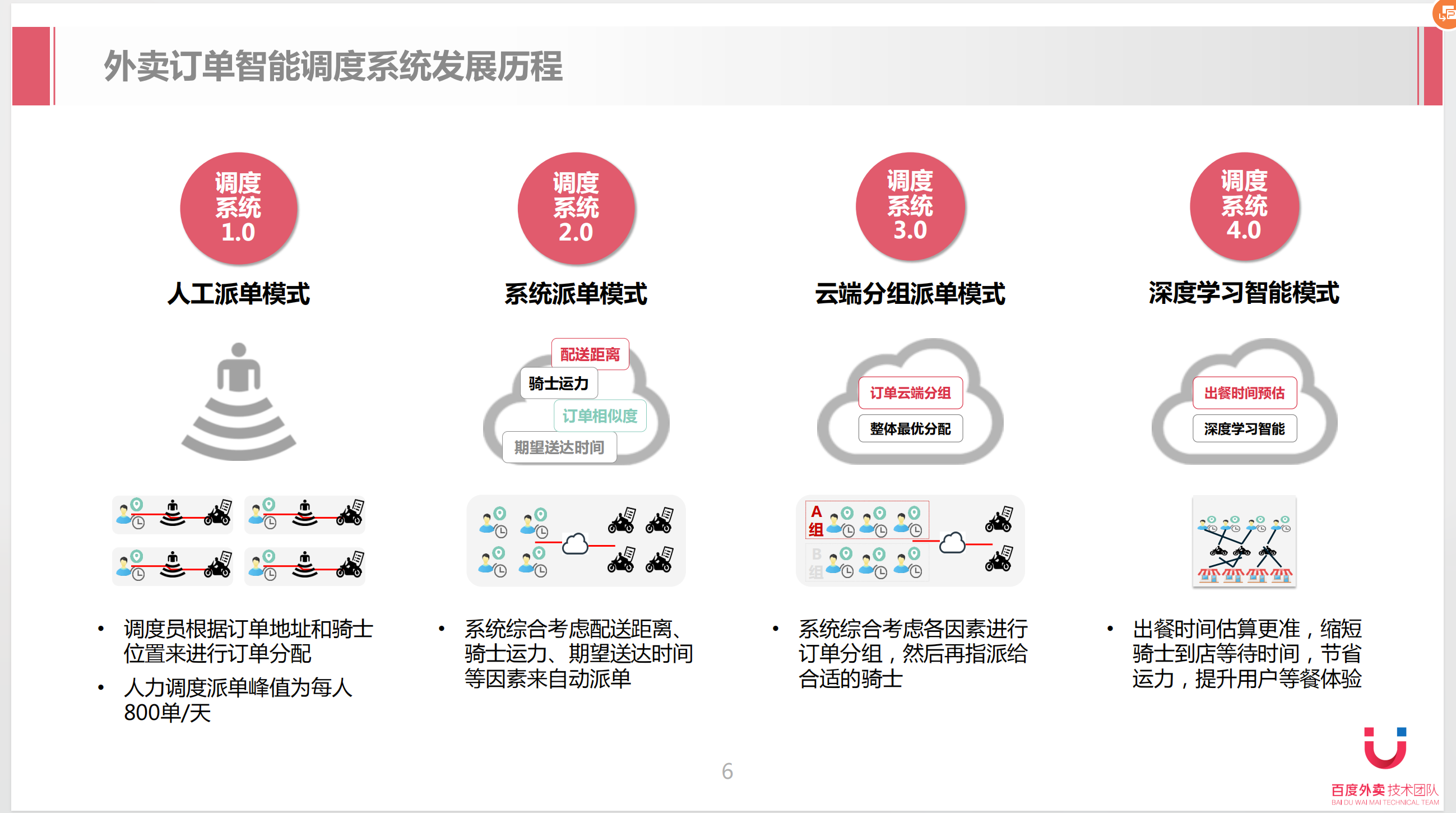
资源调度机制，在互联网和制造业领域有很广泛的应用，例如像外卖系统、滴滴打车系统以及车间调度系统，都涉及到人力和机器的资源调度，这块更是这些厂家的核心技术所在。例如下面百度外卖技术团队分享的外卖订单调度系统、以及某个厂家的车间调度系统。

资源调度要从两个出发点进行考虑：

• 对企业来说，最关心的是成本问题，所以要有效协调和分配资源，来降低成本
• 对用户（流程服务的用户）来说，服务质量放在首位，所以需要降低流程的总执行时间

所以，资源调度既可以对资源进行有效的协调和分配，降低企业的成本；又能快速、准确地完成任务，给用户一个更好的用户体验。要在两者之间实现一个很好的平衡，这就是资源调度算法要做的事情。

如果工作项的启动交互是由用户发起的，那么参与者必须从其分配的队列中手动选择它来开始执行。如果启动交互是由系统启动的，则工作项将自动启动并放在参与者的已启动队列中执行操作。

在工作项的初始分配完成后，拥有所需授权（或特权）的参与者可以进一步影响工作项的分配和执行。如果工作项目分配给他们，他/她可以重新分配（重新启动分配，从分配集中排除）；将其委派给其“团队”成员——最终向参与者的位置汇报的职位）；或跳过工作项目（无需首先启动即可立即完成）。如果工作项目已经启动，参与者可以将其重新分配（重新分配给他们的团队成员）。

BPM中的任务分配

在业务流程管理（Business Process Management，简称BPM）中，任务分配是一个关键的环节，它决定了资源如何被有效地分配和使用。这个过程通常涉及到以下几个步骤：

• 资源定义：在BPM中，资源可以是人、设备、物料或者时间等。在定义资源时，需要明确每种资源的特性，如可用性、能力、成本等，也就是要把资源的能力量化。
• 任务定义：定义工作流中的每一个任务，包括任务的类型、所需的资源、优先级、截止时间等。
• 资源分配策略：定义资源分配的策略，如基于优先级的分配、基于成本的分配、基于时间的分配等。这些策略可以帮助系统在多个任务之间有效地分配资源。
• 任务分配：根据资源分配策略，将任务分配给相应的资源。这个过程可以是自动的，也可以是手动的。

在BPM系统中，还可以通过设置角色和权限来控制资源的访问和使用。例如，可以设置只有特定角色的用户才能访问某个资源，或者只有特定角色的用户才能执行某个任务。这样可以保证资源的安全性，同时也可以提高工作流的效率。

此外，BPM系统还可以通过数据分析和报告功能，帮助管理者了解资源使用的情况，从而做出更好的决策。例如，可以通过分析报告发现哪些资源被过度使用，哪些资源被闲置，然后调整资源分配策略，以提高资源的利用率。

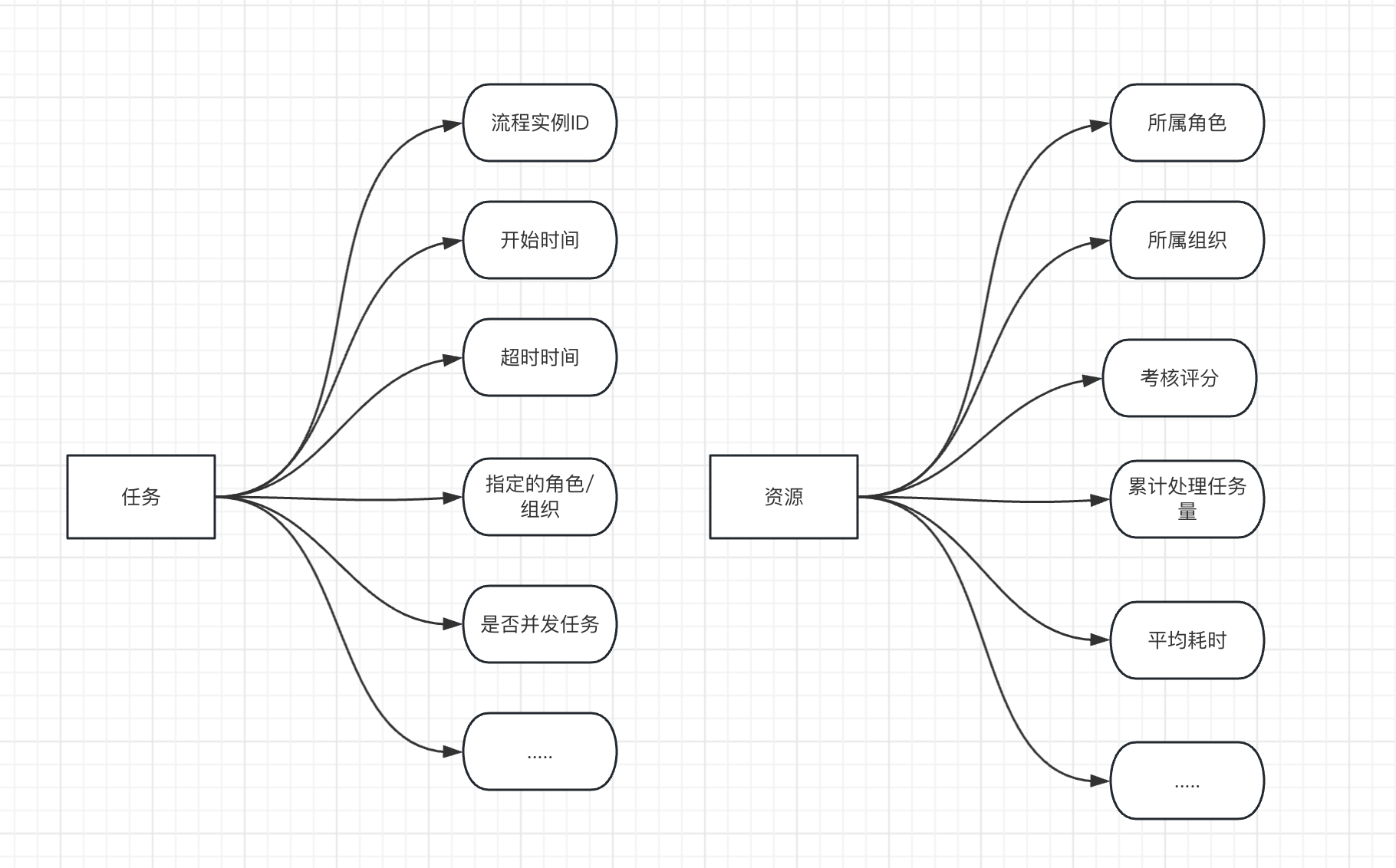
资源与类别

资源

资源是指可以执行某些任务的人或机器（可以物理的机器设备或软件里的AI机器人）。一般我们本书中谈论资源的时候，默认都是指人。

当然在目前大模型的推动下，AI逐渐具备了基础的世界知识，以及专业领域的知识，例如GPT3.5和GPT4。而且现在的AI机器人已经具备跟人类高中水平以上的理解能力，可以在很多地方上逐渐替代人类的角色来实现完全的自动化处理任务。

资源类别

资源类别是指一组具有共同特征的资源集合。例如我们说老师这个资源或销售这个资源类别。

常见的资源类别可以基于下面几种方式来定义：

• 角色：基于能够做什么，一般具有相同的技能。
• 组织：基于组织信息，一般在相同的组织架构下。

资源分配模式

常见的资源分配模式包括创建模式、推模式、拉模式等。下面分别对这几种模式进行介绍：

• 创建模式（Creation Patterns）：在创建模式中，任务的创建者会直接指定任务的执行者。这种模式适用于明确知道谁负责执行某个任务的情况。创建模式可以实现对任务执行者的精确控制，但缺点是灵活性较差，不适合处理动态变化的任务分配需求。

  创建模式可以根据任务分配的依据细分为以下几类：

  1. 直接分配：创建者直接将任务分配给指定的个人。这种方式最为简单，适用于任务执行者固定且明确的情况。
  2. 角色分配：创建者将任务分配给具有特定角色的人员。这种方式适用于任务需要特定角色的人员来完成，但具体执行者可以灵活选择。
  3. 组织分配：创建者将任务分配给特定的组或部门。这种方式适用于任务需要由某个组或部门的成员来完成，但具体执行者可以在组内进行协商和调整。
  4. 职责分离模式：两个任务之间存在一个约束，要求它们在给定的流程实例中不由同一用户执行。例如，签署支票任务不能由完成提交采购订单任务的同一用户来执行。
  5. 基于能力的分配：根据资源所具备的能力，将任务提供或分配给一个或多个资源。例如，将审计帐户任务分配给具有注册会计师资格的用户。
  6. 基于历史的分配：根据资源之前的执行历史，将任务提供或分配给一个或多个资源。例如，将审计大客户任务分配给过去三个月中完成最多审计的用户。

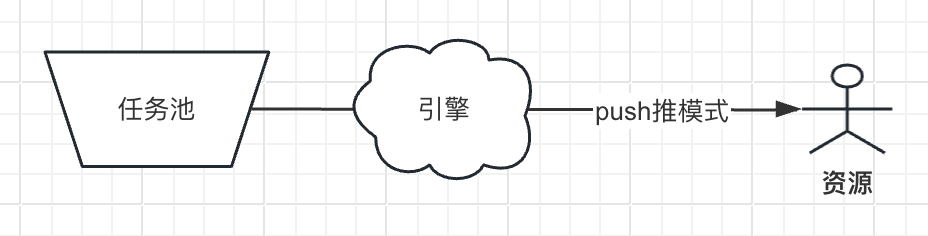
• 推模式（Push Patterns）：推模式下，引擎会主动将任务分配到资源。也就是把任务和资源进行匹配，但是资源自身不能选择，一旦一个资源（人）执行完一个任务，就会被引擎立刻分配一个新的任务，类似我们生活中美团送外卖的和滴滴司机的情况。推模式可以实现任务的自动分配，提高工作流的执行效率。然而，这种模式可能导致任务分配不均衡，因为执行者无法主动选择任务，只能被动接受。

  注意，在这种模式下引擎的操作对象有两个，一个是任务，另一个是资源（人）。所以这里操作分两个步骤：

  • 首先是决定要处理哪个任务先，即任务的排队顺序。
  • 然后是决定把前面的任务分配给哪个资源，即资源的排队顺序，到这里才是开始推模式。

  所以推模式下，引擎需要进行任务排队和资源排队，形成两个队列后，再进行分配。

  

  任务排队原则

  1、先进先出(FIFO)：这是一种最基本的资源分配模式，也被称为先来先服务(FCFS)。简单来说，它就是先到达的任务请求先被处理。这种方式公平且简单，但可能导致某些需要大量资源的请求阻塞后续的小请求。

  2、后进先出(LIFO)：与FIFO相反，LIFO策略是最后到达的请求先被处理。这种方式在某些情况下可能会导致资源的更高效使用，但也可能导致一些任务请求无限期地等待。

  3、最短处理时间(SPT)：在这种模式下，处理时间最短的任务请求优先得到服务。这种方式可以最小化总的等待时间和系统中的任务数量，但可能会导致长任务饿死，即长任务永远无法得到处理。

  4、最短剩余处理时间(SRPT)：这是SPT的一种变体，其中优先级最高的是剩余处理时间最短的任务请求，而不是总的处理时间最短的任务请求。这种方式可以进一步减少等待时间和系统中的任务数量，但同样可能导致长任务饿死。

  5、最早截止期限(EDD)：在这种模式下，最早截止的任务请求优先得到服务。这种方式在处理有截止期限的任务时非常有效，可以最小化未按时完成的任务数量。然而，它可能导致一些没有截止期限的或截止期限较晚的任务长时间得不到处理。

  资源排队原则

  1. 单一资源分发模式：任务以非强制的方式提供给指定的单一资源。例如，审查反馈任务提供给用户smith，但他们没有义务去完成它。
  2. 多资源分发模式：任务以非强制的方式提供给多个资源，期望其中一个资源可能会承担起来。例如，流程申请任务提供给管理员角色的成员，尽管他们没有义务去完成它。
  3. 单一资源分配模式：任务以强制的方式分配给指定的单一资源，并且他们预期在未来的某个时间完成它。
  4. 随机分配模式：从一组资源中随机选择一个资源分配任务。例如，将流程申请任务随机分配给管理员角色的一个成员。
  5. 轮流分配模式：从一组资源中按照轮流的方式选择一个资源分配任务。例如，将流程支持请求任务分配给最近最少执行该任务的系统管理员角色的成员。
  6. 最短队列模式：根据谁的待处理工作最少（即工作队列最短）从一组资源中选择一个资源分配任务。例如，将年度审查任务分配给待处理工作最少的系统管理员角色的成员。

  注意：这里分发是自愿性的，而分配则带有强制性的。

  前面介绍的6种原则都是比较简单的模式，还有一些更加高级的调度算法，例如我们后面会介绍的遗传算法，以及蚁群算法、粒子群算法、模拟退火算法在车间调度问题上的解决。还有一些甚至可以使用深度学习的AI算法来进行调度分配。

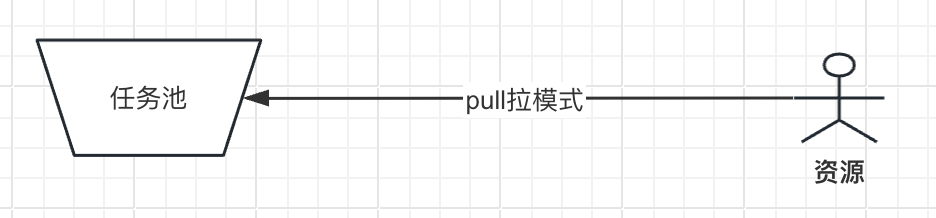
• 拉模式（Pull Patterns）：在拉模式中，任务会被放入一个公共的任务池，合适的执行者可以从任务池中主动领取任务。这种模式允许执行者根据自己的能力和负载情况来选择任务，有利于实现任务的平衡分配。但是，拉模式可能导致任务执行的不确定性，因为任务的领取和完成时间可能受到执行者的主观因素影响。

  

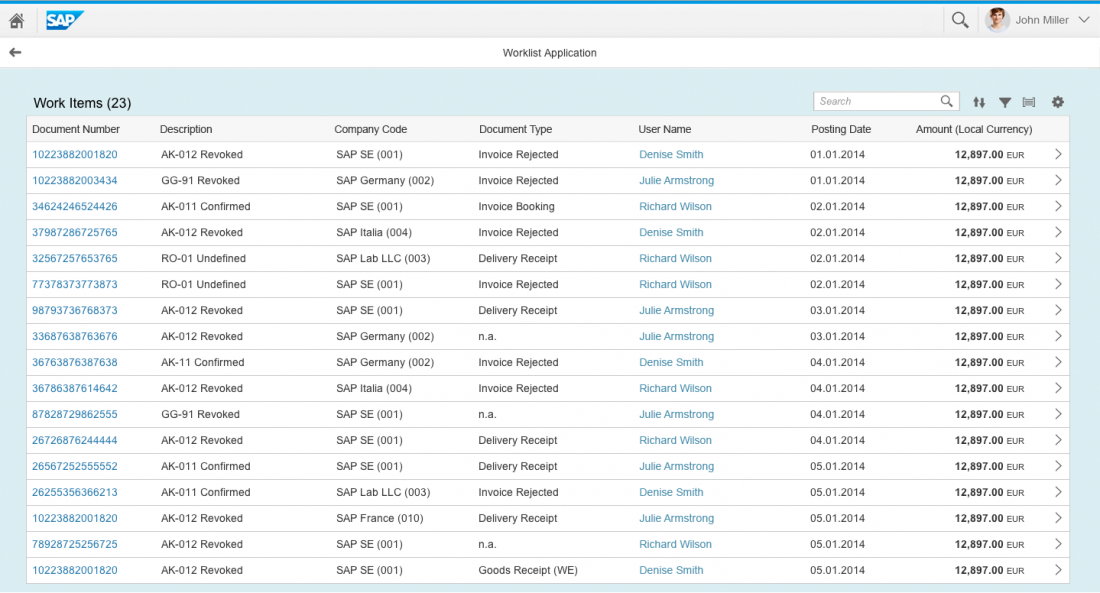
  资源能够对他们看到和/或可以承担的工作项的顺序施加排序/重新排序。例如，按接收日期顺序重新排序工作项，并选择他们接下来要承担的工作项。即每个资源（人）都有一个工作任务列表，类似像SAP的Work Items。

  

• 自动执行模式（Automatic Execution）：工作项可以在不需要分配给资源的情况下执行。例如，发送订单工作项可以在不需要用户完成的情况下自动执行。

一般情况下，我们可以采取介于推模式和拉模式之间的方法，采用拉模式，即员工主动领取任务为主。同时用工作流引擎的推模式生成任务的计划安排（甘特图）作为辅助手段。

资源调度框架

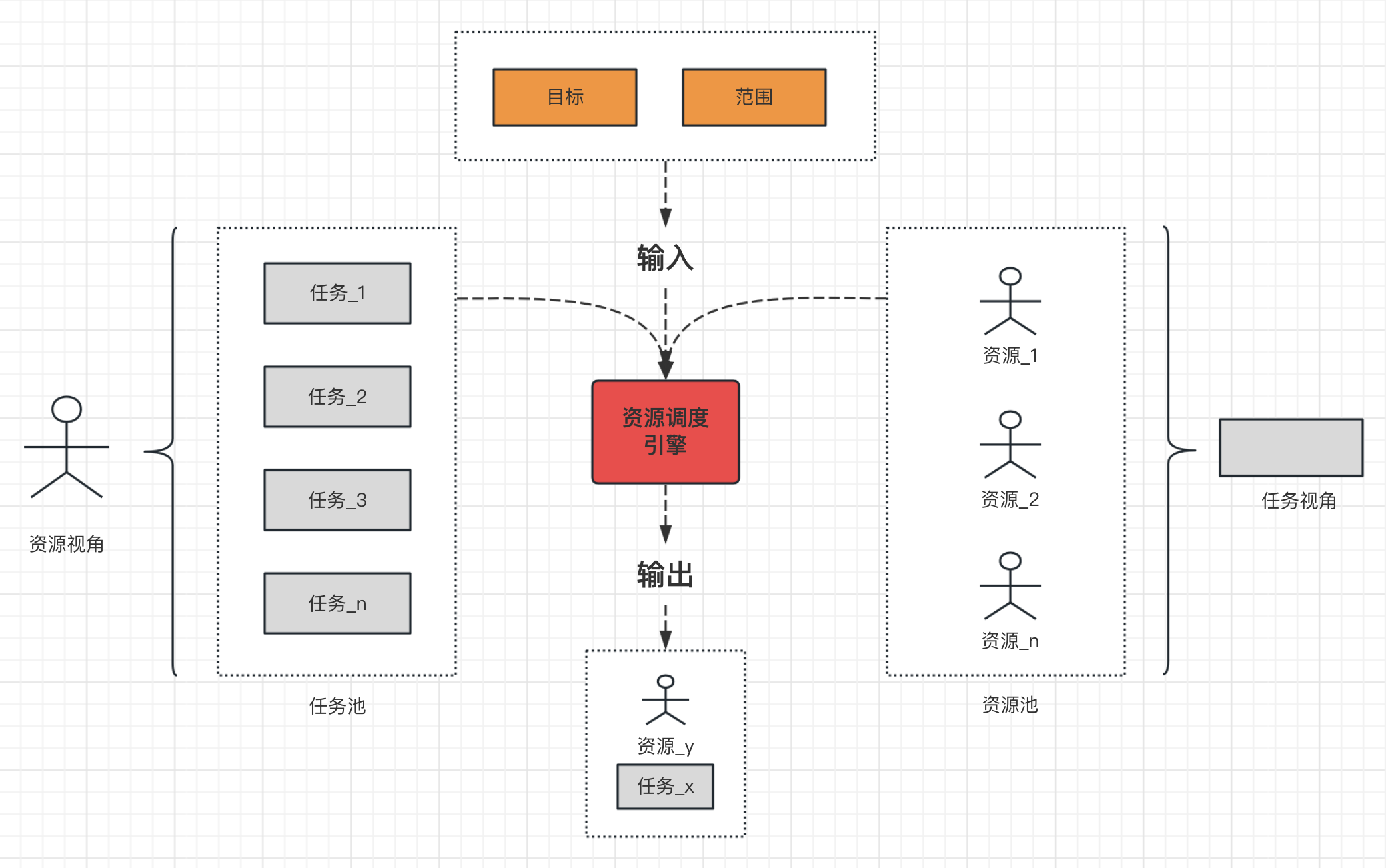
输入：

• 当前有哪些任务待分配资源

• 当前有哪些资源可使用

• 目标：基于成本最优、基于时间最优等

• 范围：指定角色、组织、技能范围

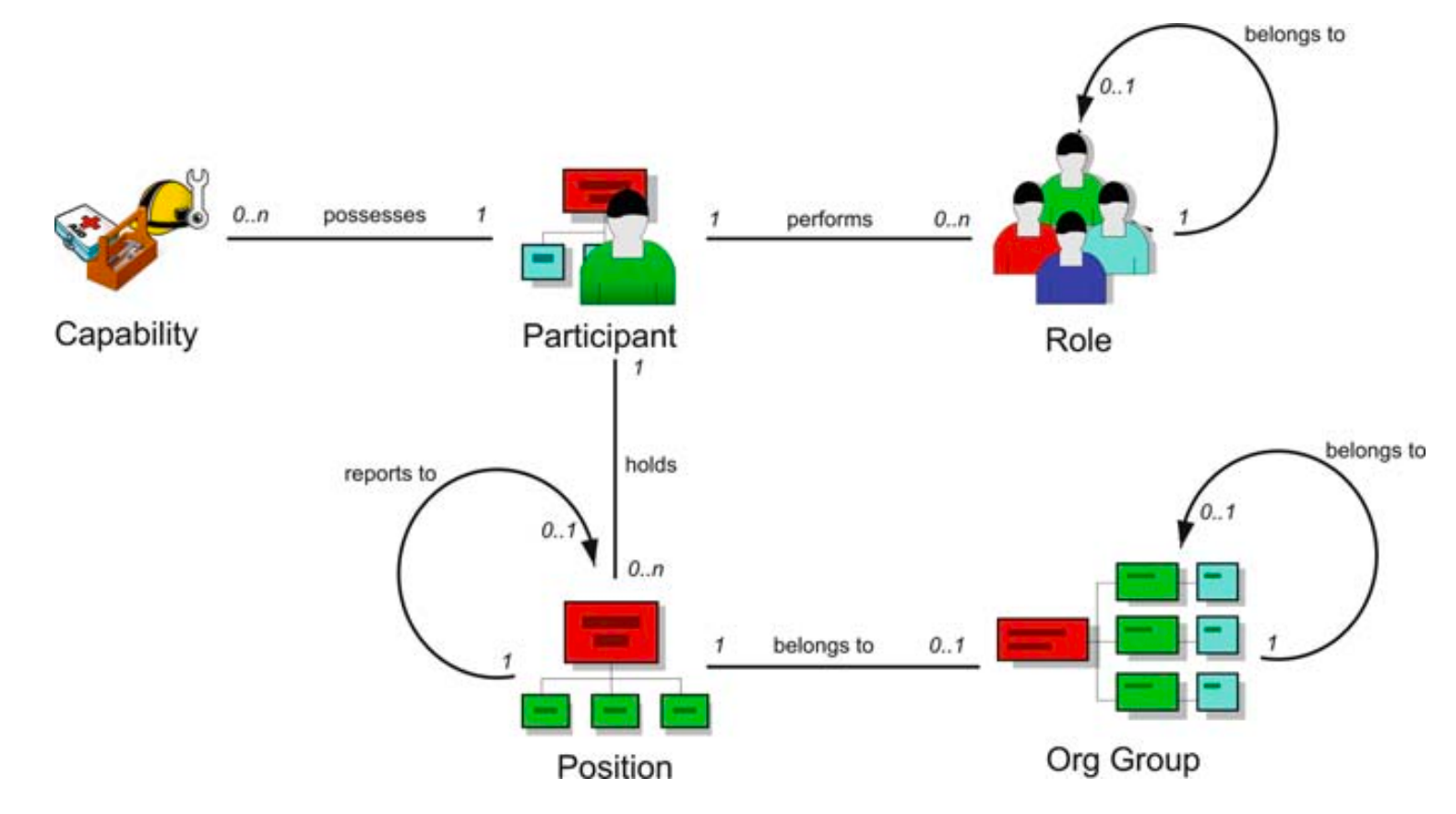
  在一个流程中，参与者、角色、技能、组织之间关系的一种结构化模型。这里提到的组织模式，是用于描述参与者（human resources）在流程中的组织结构和关系的模型。

  

输出：

• 每个任务对应分配了哪个资源

引擎的输出其实就是一个甘特图，这个甘特图可以看到过去、现在以及未来所有资源和任务的分配情况。

下面的f就是资源分配的策略：

f(当前有哪些任务待分配资源,当前有哪些资源可使用，目标，权限) = 哪个任务对应分配了哪个资源

兑入资源调度系统，每次输入的时候可以看到如下一个二维表，其输出就是根据设定的目标和权限，来把任务分配到具体资源下面。

资源分配	Resource_1	Resource_2	Resource_3	Resource_4	Resource_5
Task_1
Task_2
Task_3
Task_4
Task_5

当然，每个任务Task有自身的一些运行时的上下文信息；每个资源也有一些量化的属性，例如平均执行耗时、累计历史执行任务量，所属角色等。

f调度策略什么时候被唤醒执行：

• 每次有新的任务进入待处理任务池

• 每次资源完成一个任务，重新进入可用资源池

车间调度问题

上面提及的资源调度问题，通过进一步分析，本质上其实就是车间调度问题。

作业车间调度问题（Job Shop Scheduling Problem，JSP）是一类组合优化问题，主要涉及在一个车间或工厂中，有一组作业（jobs）需要在一组机器（machines）上完成一系列任务。每个作业由多个任务组成，而每个任务都必须按照特定的顺序在不同的机器上执行。每个任务有一个预定的处理时间，而每台机器在任意时刻只能处理一个任务。问题的目标是找到一种调度方案，以最小化总体完成时间、最大化生产效率，或者满足其他特定的调度目标。

形式化地，作业车间调度问题可以定义如下：

1. 有限的机器集合： 给定一组机器 $M = {M_1, M_2, ..., M_m}。
2. 有限的作业集合： 给定一组作业 $J = {J_1, J_2, ..., J_n}。
3. 每个作业包含多个任务： 每个作业 $J_i 由一系列任务 O_{i1}, O_{i2}, ..., O_{ip} 组成。
4. 每个任务具有处理时间： 每个任务 O_{ij} 在机器上需要一定的处理时间 p_{ij}。
5. 机器约束： 每台机器在任意时刻只能执行一个任务。

问题的目标是找到一个合理的调度，使得所有作业的完成时间最小。完成时间可以是作业的总加权完成时间、最大完成时间等，具体取决于问题的特定要求。由于作业车间调度问题属于 NP-难问题，通常需要使用启发式算法或其他优化技术来找到接近最优解的调度方案。

通过上面车间调度问题的定义，我们可以发现流程中的资源调度问题本质上就是车间调度问题，只不过作业变成了流程、机器变成了资源（例如人），且作业跟流程一样其内的任务是有先后顺序的。不同的机器设备对应着流程中不同角色/组织/技能的资源。而任务的预定处理时间，就是流程中任务的平均处理时间（通过历史计算），两者的目标都是为了最小化完成时间。

如下是一个简化的例子，假设存在三个资源（R_1、R_2、R_3），以及三个流程（流程_1、流程_2、流程_3）。每个流程包含三个任务，需要分配不同的资源执行，其中每个任务都有预定的平均处理时间：

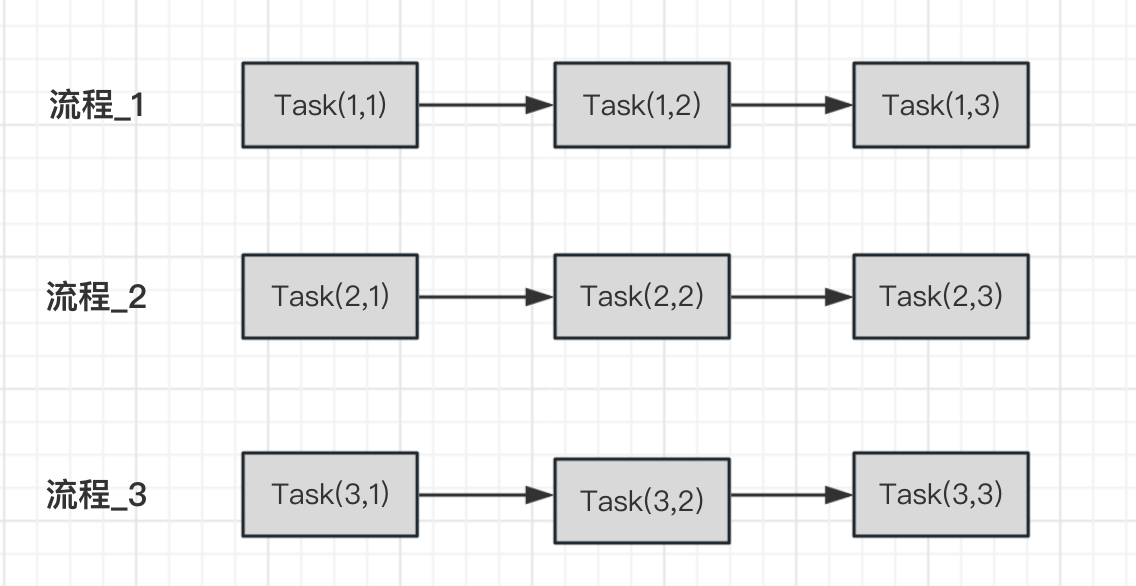
每个任务的加工顺序和需要的资源类型如下表所示：

	顺序 1	顺序 2	顺序 3
流程_1	R_3	R_1	R_2
流程_2	R_2	R_3	R_1
流程_3	R_2	R_1	R_3

下表是每个流程的任务在3个资源上处理的耗时：

	R_1耗时/h	R_2耗时/h	R_3耗时/h
流程_1	4	2	7
流程_2	3	5	6
流程_3	2	4	3

如下是调度的Gant图：

在t=0h时刻，甘特图、任务池和资源池如下所示。这时Task(2,1)和Task(3,1)都需要资源2(R_2)执行，但是由于资源同一时刻只能执行一个任务，所以在t=0h时刻只有2个任务在执行。

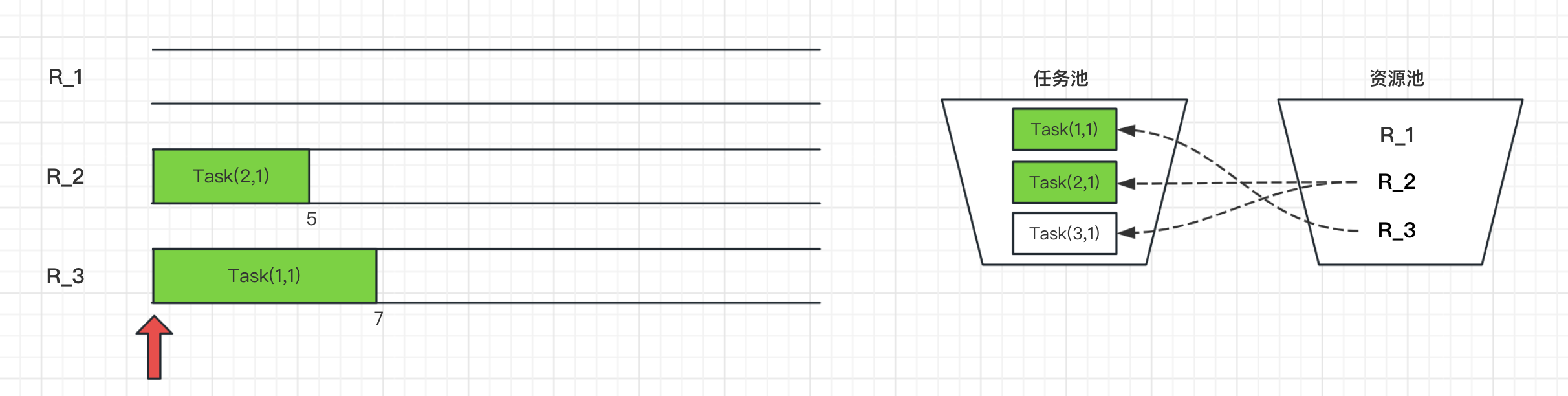
在t=5h时刻，这时Task(2,1)已经执行完，接着Task(2,2)进入任务池，同时资源R_2空闲出来也进入资源池，而资源R3由于还在执行Task(1,1)任务所以还在占用状态。此时资源池可用资源就有资源R_1和R_2，任务池待处理的有Task(2,2)和Task(3,1)。由于Task(2,2)需要资源R_3来执行，所以这次没有分配到资源。而任务Task(3,1)需要的资源R_2空闲，则可以分配执行。

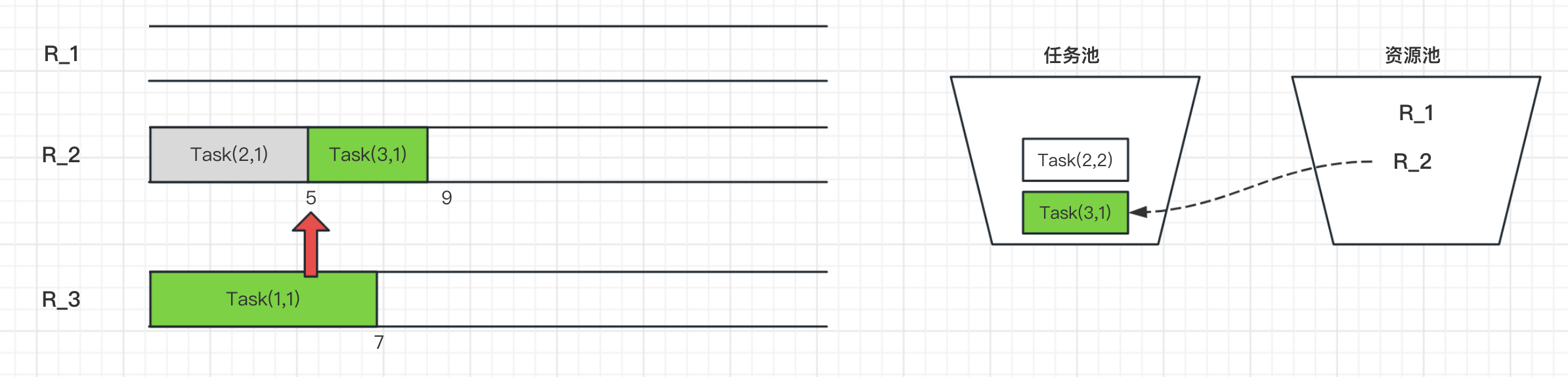
在t=7h时刻，此时任务Task(1,1)结束，接着的Task(1,2)任务进入任务池，同时资源R_3释放出来进入资源池。

此时任务池有Task(1,2)和上一次未被执行的Task(2,2)，资源池有资源R_1和R_3。

而Task(1,2)需要资源R_1，Task(2,2)需要资源R_3，刚好两者都空闲，可以分配执行。

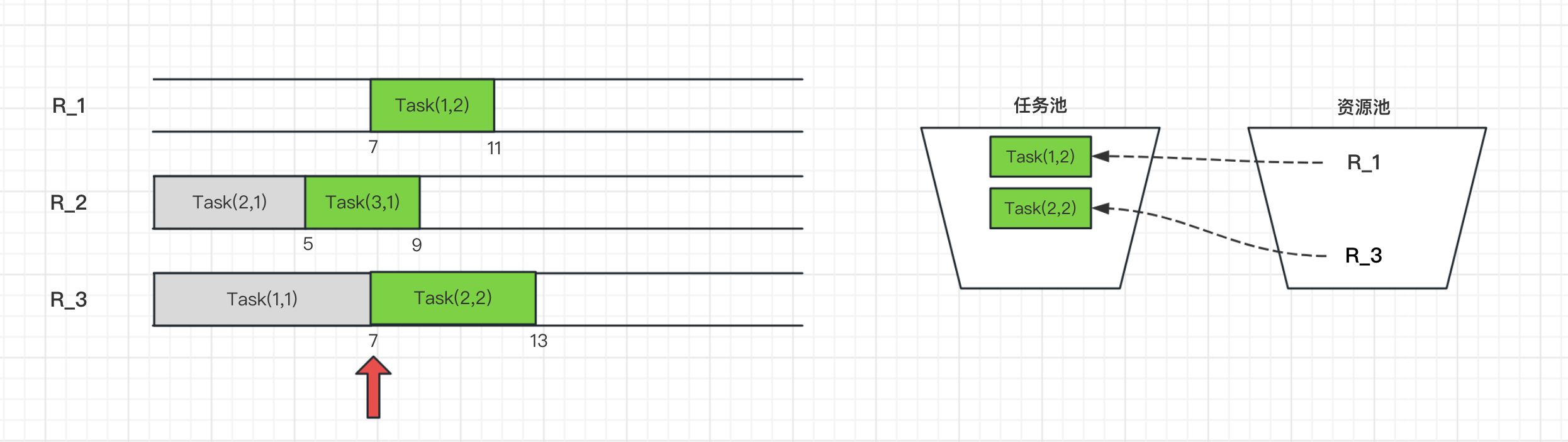
在t=9h时刻，任务Task(3,1)结束，接着Task(3,2)进入任务池，此时R_2资源释放进入资源池。

此时任务池有Task(3,2)，资源池有R_2。

但是由于Task(3,2)需要资源R_1来执行，而此时R_1正在执行Task(1,2)，所以无法分配执行。

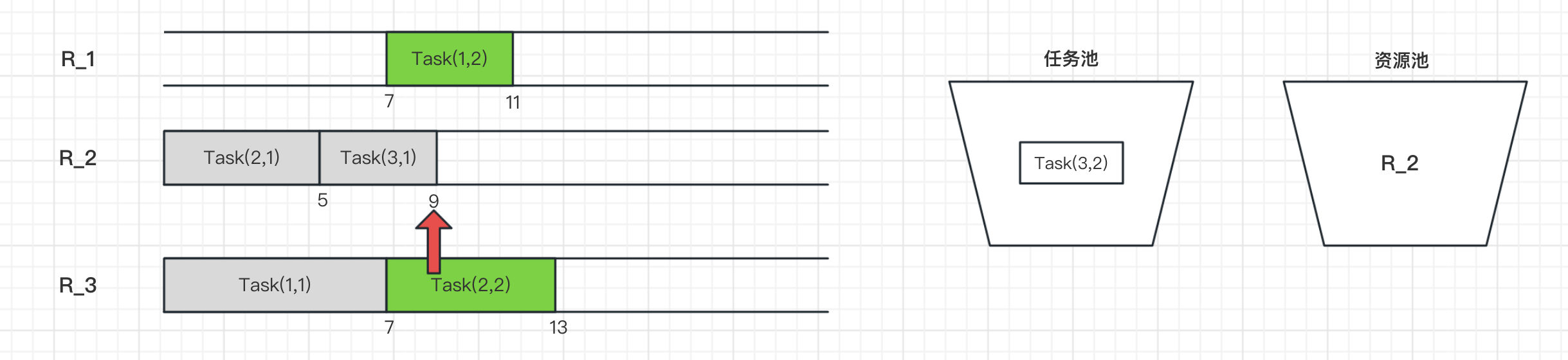
在t=11h时刻，任务Task(1,2)结束，接着的Task(1,3)进入任务池，资源R_1释放进入资源池。

此时任务池有Task(1,3)和Task(3,2)，资源池有R_1和R_2。

而Task(1,3)需要资源R_2，Task(3,2)需要资源R_1，两者正好匹配可以执行。

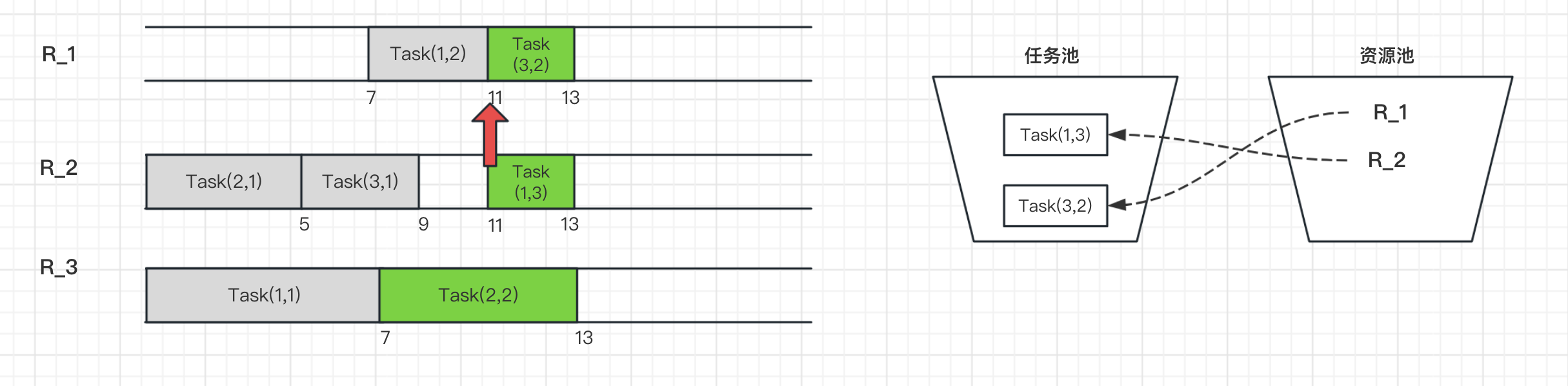
在t=13h时刻，此时Task(3,2)、Task(1,3)、Task(2,2)都结束，接着的Task(3,3)、Task(2,3)进入任务池，资源R_1、R_2和R_3都释放进入资源池。

而Task(2,3)需要资源R_1，Task(3,3)需要资源R_3，两者正好匹配可以执行。

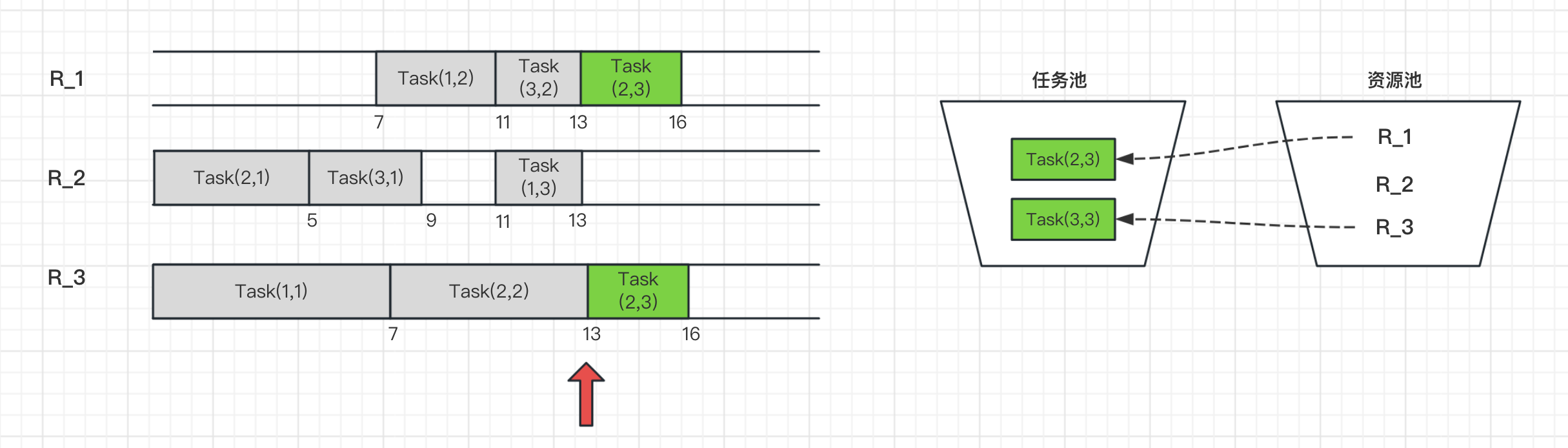
在t=16h时刻，此时所有任务都结束，任务池为空，资源都释放进入资源池。

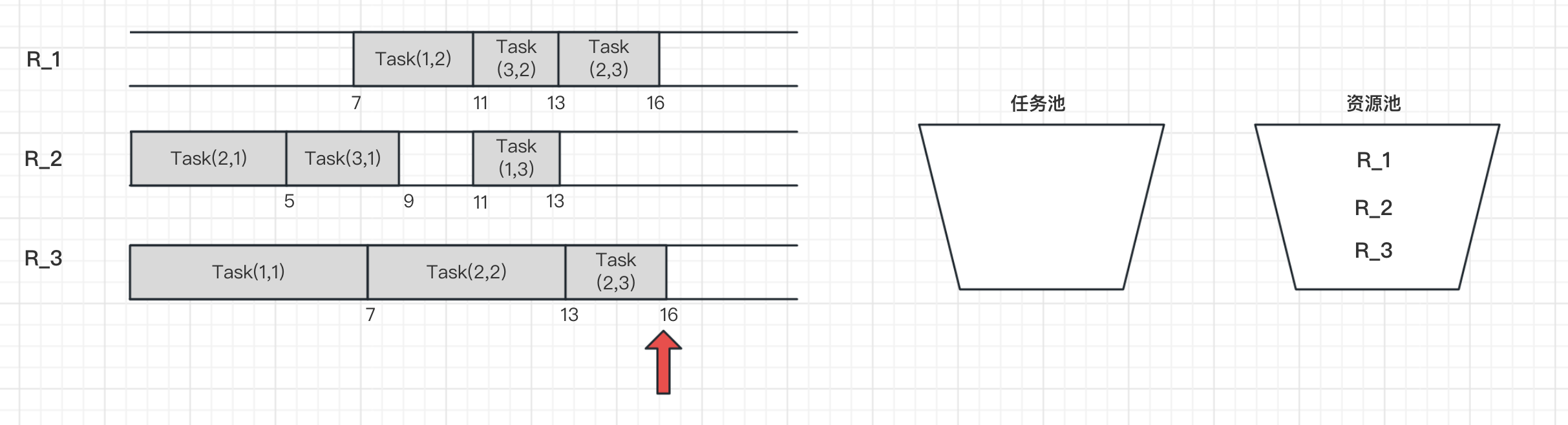
车间调度问题被证明是属于NP难问题，是数学界公认的最困难的组合优化问题之一，要获得最优解是非常困难的。所以在实际工程实践中，最好的做法是放弃寻找最优解，转而试图在合理、有限的时间内寻找到一个近似的、有用的局部最优解，例如：模拟退火、遗传算法、神经网络、深度学习等。

资源调度算法

由于作业车间调度问题的复杂性，传统的精确求解方法在大规模问题上可能效率低下。因此，启发式算法被广泛应用于解决作业车间调度问题，以寻找近似最优解。

启发式算法是一类用于解决复杂优化问题的搜索算法，它们通过模拟自然界的启发式规则或者经验性的知识，寻找问题的近似最优解。与传统的精确算法不同，启发式算法通常在可接受的计算时间内，以近似的方式找到解决方案，尤其在面对大规模、高维度或非线性的优化问题时表现出色。

一些常见的启发式算法包括：

• 遗传算法（Genetic Algorithms）： 模拟生物进化过程，通过交叉、变异等操作产生新的解。
• 模拟退火算法（Simulated Annealing）： 模拟物质退火过程，以概率的方式接受比当前解更差的解，有助于跳出局部最优。
• 粒子群优化算法（Particle Swarm Optimization）： 模拟群体中个体的协作和信息传递，通过更新个体的位置来搜索最优解。
• 蚁群算法（Ant Colony Optimization）： 模拟蚂蚁在寻找食物过程中的信息传递和路径选择，用于解决路径规划等问题。

遗传算法

遗传算法（Genetic Algorithm，简称GA）是一种受自然选择和遗传学理论启发的优化算法。它模拟了生物进化的过程，通过对个体的遗传信息进行进化和交叉，以产生更好的解决方案。遗传算法主要用于解决搜索和优化问题，特别是那些复杂、多变的问题，如组合优化、参数优化、机器学习等领域。

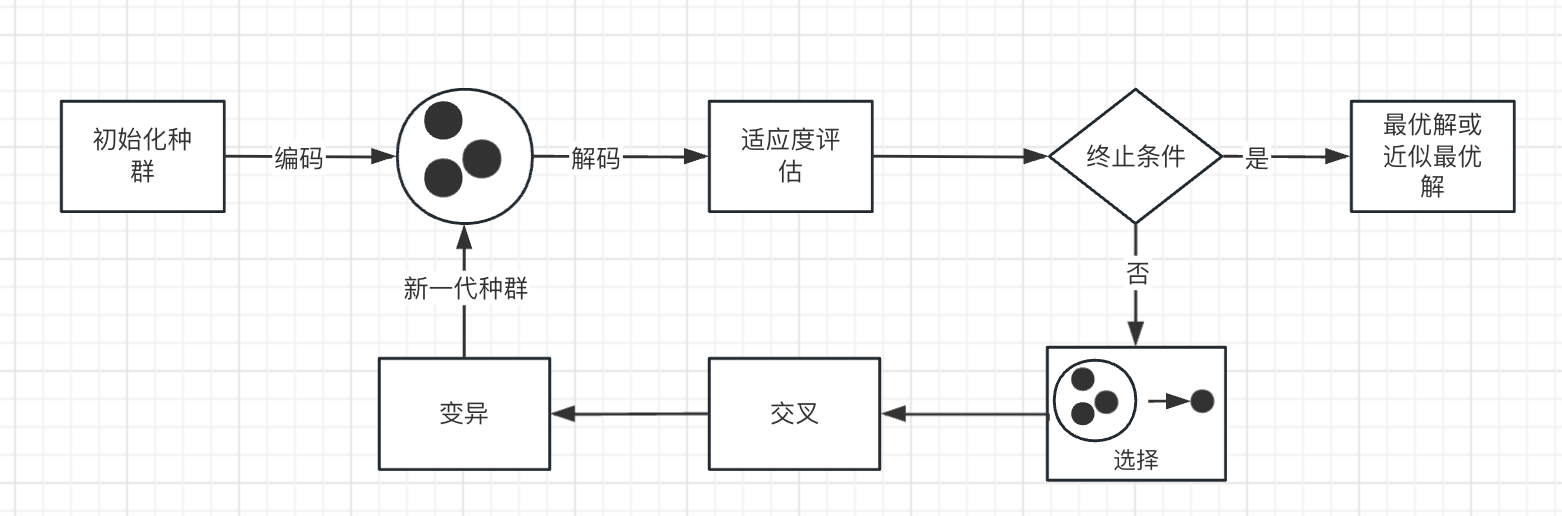
以下是遗传算法的基本步骤：

1. 初始化种群： 随机生成一组个体，每个个体都是问题的一个可能解。
2. 适应度评估： 对每个个体计算其适应度，即解决问题的质量。适应度函数根据问题的性质而定，通常是目标函数的值。
3. 选择： 通过某种选择策略，选择适应度较高的个体作为父代，用于产生下一代。
4. 交叉： 随机选择一对父代个体，通过交叉操作产生子代。交叉操作模拟了基因的重组过程。
5. 变异： 对子代进行变异操作，以引入新的遗传信息。变异操作模拟了基因发生突变的情况。
6. 替换： 用新生成的子代替代老一代，形成新的种群。
7. 重复： 重复上述步骤直到达到停止条件，如达到最大迭代次数或找到满足要求的解。

如下图所示是遗传算法的关键流程，其中编码（Encoding）和解码（Decoding）是两个关键步骤，它们分别用于将问题的解表示成染色体串（Chromosome）和从染色体中提取出问题的解。

• 编码：编码是将问题的解（Solution）转换为染色体的过程，它是将问题的解空间映射到遗传算法的搜索空间。编码的目的是为了实现交叉、变异等类似生物界的遗传操作。必须考虑染色体的合法性、可行性、有效性，以及对问题解空间表达的完全性。良好的编码方式在后续遗传操作中易产生可行解，提高执行效率。
• 解码：解码是从染色体中提取出问题的解的过程。它是编码过程的逆向操作。当遗传算法找到一个可能的解（即染色体）时，需要将这个染色体解码为实际的问题解。解码过程需要确保解码出的解在问题的解空间中是有效的。

遗传算法的优势在于能够在大规模、复杂的搜索空间中找到全局最优解或接近最优解。它灵活适用于不同类型的问题，并且相对于一些传统的优化算法更具鲁棒性。

遗传算法的应用领域包括但不限于：

• 组合优化问题：如旅行商问题（TSP）、背包问题等。
• 函数优化：寻找函数的最大或最小值。
• 机器学习：参数优化、特征选择等。
• 调度问题：优化任务分配和资源调度。
• 进化计算：模拟生物进化过程，用于生成人工生命体等。

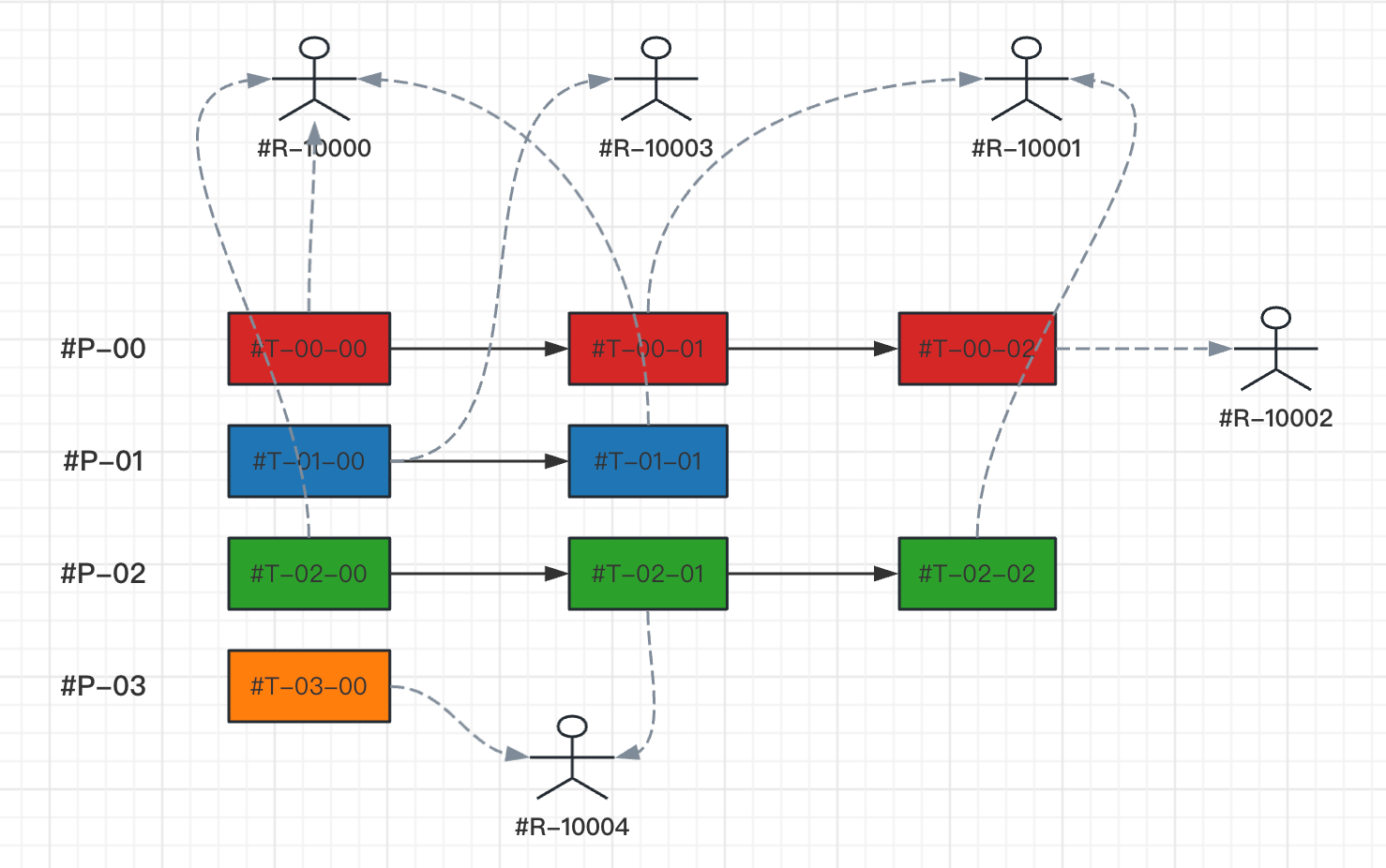
如下是4个流程以及流程中各个任务需要的资源，接下来，我们使用遗传算法来对这些任务和资源进行合理分配，得到一个总耗时最小时间的调度计划。

根据前面遗传算法的介绍，一个遗传算法有以下几个关键的步骤：

class GA:
  # 初始化参数
  def __init__(self):
    pass
  # 初始化种群
	def init_population(self):
    pass
  
  # 适应度评估
  def get_fitness(self):
    pass
  
  # 选择
  def select(self):
    pass
  
  # 交叉
  def crossover(self):
    pass
  
  # 变异
  def mutate(self):
    pass
  
  # 重复上述过程知道满足条件为止
  def run(self):
    pass

接下来，我们一步步来实现上述关键的函数功能。

编码

如前所述，资源调度问题包括两个子问题:资源选择和任务排序。

• 资源选择解决每个任务在可选资源集中的哪个资源上进行执行的问题。
• 任务排序解决所有任务确定资源后的排序和开始执行时间问题。

在进行后续步骤以前，我们需要对实际问题进行编码操作，转换成遗传算法可以理解执行的染色体，即将实际问题解空间的搜索编码转换成染色体，而每一个染色体即表示问题的一种可能解。

下面我们采用任务排序进行编码， 其编码方式如下图所示:

染色体编码为:chromosome = ...,wi,wj,wk,...，其中wi代表第i个顺序流程，而流程出现的次数代表流程的第几个任务。

例如：chromosome=[1,3,3,3,2,2,2,0,0]中0、1、2、3表示流程的顺序编号，例如我们分别对应上面的#P-01、#P-03、#P-02、#P-00四个流程，并且第几次出现就代表流程的第几个任务。然后将每一次随机生成的染色体个体加入到种群集合中，这个种群中每一个染色体都是问题的解，我们通过适应度来评估每一个染色体。

例如流程的顺序编号映射关系如下：

注意：顺序编号跟流程编号的映射关系是在初始化时随机的。

流程编号	#P-01	#P-03	#P-02	#P-00
顺序编号	0	1	2	3

例如染色体编码的映射关系：

染色体	1	3	3	3	2	2	2	0	0
流程编号	#P-03	#P-00	#P-00	#P-00	#P-02	#P-02	#P-02	#P-01	#P-01
任务编号	#T-03-00	#T-00-00	#T-00-01	#T-00-02	#T-02-00	#T-02-01	#T-02-02	#T-01-00	#T-01-01

我们将前面的4个流程转换成如下的数组表示，通过该数组可以知道流程的任务顺序以及每个任务的执行耗时。

data = [{'process': '#P-00', 'task': '#T-00-00', 'resource': '#R-10000', 'time': 10, 'order': 0},
         {'process': '#P-00', 'task': '#T-00-01', 'resource': '#R-10001', 'time': 21, 'order': 1},
         {'process': '#P-00', 'task': '#T-00-02', 'resource': '#R-10002', 'time': 12, 'order': 2},

         {'process': '#P-01', 'task': '#T-01-00', 'resource': '#R-10003', 'time': 21, 'order': 0},
         {'process': '#P-01', 'task': '#T-01-01', 'resource': '#R-10000', 'time': 21, 'order': 1},

         {'process': '#P-02', 'task': '#T-02-02', 'resource': '#R-10001', 'time': 5, 'order': 2},
         {'process': '#P-02', 'task': '#T-02-01', 'resource': '#R-10004', 'time': 11, 'order': 1},
         {'process': '#P-02', 'task': '#T-02-00', 'resource': '#R-10000', 'time': 10, 'order': 0},

         {'process': '#P-03', 'task': '#T-03-00', 'resource': '#R-10004', 'time': 5, 'order': 0}]

上面的原始数据还需要进一步调用reshape_data方法进行加工，转换成遗传算法能处理的数据形式。

def reshape_data(data: List[Dict]) -> ReshapeData:
    '''
    将输入数据转换为遗传算法可以处理的格式，结果包括转换后的数据、流程、资源、任务等信息。
    '''
    def make_array(r: dict) -> ReshapeData:

        '''
        变量r的数据结构如下案例所示：
        {
            '#P-00': [
                {'process': '#P-00', 'task': '#T-00-00', 'resource': '#R-10000', 'time': 10, 'order': 0}, 
                {'process': '#P-00', 'task': '#T-00-01', 'resource': '#R-10001', 'time': 21, 'order': 1}, 
                {'process': '#P-00', 'task': '#T-00-02', 'resource': '#R-10002', 'time': 12, 'order': 2}
                ], 
            '#P-01': [
                {'process': '#P-01', 'task': '#T-01-00', 'resource': '#R-10003', 'time': 21, 'order': 0}, 
                {'process': '#P-01', 'task': '#T-01-01', 'resource': '#R-10000', 'time': 21, 'order': 1}
                ], 
            '#P-02': [
                {'process': '#P-02', 'task': '#T-02-02', 'resource': '#R-10001', 'time': 5, 'order': 2}, 
                {'process': '#P-02', 'task': '#T-02-01', 'resource': '#R-10004', 'time': 11, 'order': 1}, 
                {'process': '#P-02', 'task': '#T-02-00', 'resource': '#R-10000', 'time': 10, 'order': 0}
                ], 
            '#P-03': [
                {'process': '#P-03', 'task': '#T-03-00', 'resource': '#R-10004', 'time': 5, 'order': 0}
                ]
        }
        '''
        processs = list(set(map(lambda v: v["process"], data)))
        resources = list(set(map(lambda v: v["resource"], data)))
        task = [-1 for _ in processs]
        

        reverse_processs = make_reverse_index(processs) # 把流程编号跟数组索引id做映射
        reverse_resources = make_reverse_index(resources) # 把资源编号跟数组索引id做映射
        '''
        例如：
        reverse_processs==> <class 'dict'> {'#P-01': 0, '#P-03': 1, '#P-02': 2, '#P-00': 3}
        reverse_resources==> <class 'dict'> {'#R-10002': 0, '#R-10000': 1, '#R-10001': 2, '#R-10004': 3, '#R-10003': 4}
        '''
        ans = [-1 for _ in r.keys()] # 流程个数，这里是4个流程
 
        for process_id, task_list in r.items():
            # process_id是流程编号，task_list是流程里的任务数组
            # m取task_list任务数组中成员order值最大的值
            m = max(*map(lambda v: v["order"], task_list))  if len(task_list) > 1 else task_list[0]["order"]
            t = [-1 for _ in range(m + 1)] # t[key] = (v1,t), key为任务的顺序编号，v1为资源顺序编号，t为资源执行任务的耗时
            x = [-1 for _ in range(m + 1)] # x[key] = value，key为任务的顺序编号，value为任务编号
            for p in task_list:
                '''
                p是流程中某一个任务，例如：{'process': '#P-03', 'task': '#T-03-00', 'resource': '#R-10004', 'time': 5, 'order': 0}，
                p["resource"] = '#R-10004', reverse_resources[p["resource"]] = reverse_resources['#R-10004'] = 3
                p["time"] = 5
								p["order"] = 0
                t[p["order"]] = (reverse_resources[p["resource"]], p["time"]) <==> t[0] = (3,5)
                '''
                t[p["order"]] = (reverse_resources[p["resource"]], p["time"]) 
                x[p["order"]] = p["task"] 
            x = filter_value(x, -1) # 把key=-1的无效数组成员移除，例如：['#T-03-00', -1, ...]
            t = filter_value(t, -1) # 把key=-1的无效数组成员移除，例如：[(3,5),-1,....]
            
            ans[reverse_processs[key]] = t
            '''
            ans[key] = [(v1,t),....]，其中key是流程的顺序编号，t里的每个成员中，v1为资源顺序编号，t为资源执行任务的耗时
            '''
 
            task[reverse_processs[process_id]] = x

        task = filter_value(task, -1) # 把key=-1的无效数组成员移除，例如：[['#T-03-00'],-1,....]
        '''
        task[key] = [task_list_1,...]，其中key是流程的顺序编号，task_list表示流程对应的任务编号数组
        task==> [
            ['#T-01-00', '#T-01-01'], 
            ['#T-03-00'], 
            ['#T-02-00', '#T-02-01', '#T-02-02'], 
            ['#T-00-00', '#T-00-01', '#T-00-02']
        ]
        '''

        ans = filter_value(ans, -1)
        '''
        ans就是把所有编号表示转换成二维数组索引方式表示
        ans==> [
            [(4, 21), (1, 21)],            ---->表示顺序编号为0的流程的任务列表，即：#P-01
            [(3, 5)],                      ---->表示顺序编号为1的流程的任务列表，即：#P-03
            [(1, 10), (3, 11), (2, 5)],    ---->表示顺序编号为2的流程的任务列表，即：#P-02
            [(1, 10), (2, 21), (0, 12)]    ---->表示顺序编号为3的流程的任务列表，即：#P-00
        ]        
        一维数组成员的索引跟reverse_processs一一对应
        二维数组成员表示流程的任务在对应资源上的执行耗时，顺序是按照任务的order字段排序
        例如：
        一维数组的第一个索引成员，'#P-01': [
                {'process': '#P-01', 'task': '#T-01-00', 'resource': '#R-10003', 'time': 21, 'order': 0}, 
                {'process': '#P-01', 'task': '#T-01-01', 'resource': '#R-10000', 'time': 21, 'order': 1}
                ]
        则ans中的(4,21)，4表示资源#R-10003，表示流程#P-01的第一个任务#T-01-00在资源#R-10003上执行耗时时21
        '''
        return ReshapeData(ans, processs, resources, task, reverse_resources, reverse_processs)
 
    # 把一维数组转换成按照流程编号分组的对象数组，map[流程编号] = [...]
    result = {}
    for value in data:
        w = value["process"]
        if w in result:
            result[w].append(value)
        else:
            result[w] = [value]
    
    return make_array(result)

首先是GA类对象参数初始化，其中的resource_matrix、time_matrix和task_matrix三个成员变量主要用于辅助遗传算法中的编码和解码操作。

class GA:
    def __init__(self, population_size = 50, times = 10, cross_rate = 0.95,
                 mutation_rate = 0.05, process_number = 0, resource_number = 0):
        self.population_size = population_size  # 种群数量
        self.times = times  # 遗传代数
        self.cross_rate = cross_rate  # 交叉概率
        self.mutation_rate = mutation_rate  # 突变概率
 
        self.process_number = process_number  # 流程数量
        self.resource_number = resource_number  # 资源数量
        self.task_number: int = 0  # 任务数量
        self.chromosome_size: int = 0  # 染色体长度 = 所有流程的任务数
 
				# self.resource_matrix[i][j]表示第i个顺序流程第j个顺序任务所使用的资源编号
        self.resource_matrix = [[-1 for _ in range(MATRIX_SIZE)] for _ in range(MATRIX_SIZE)] 
    
    		# self.time_matrix[i][j]表示第i个顺序流程第j个顺序任务所用加工时间
        self.time_matrix = [[-1 for _ in range(MATRIX_SIZE)] for _ in range(MATRIX_SIZE)] 
        
        # self.task_matrix[i][j]表示第i个流程在第j台资源上的任务编号
        self.task_matrix = [[-1 for _ in range(MATRIX_SIZE)] for _ in range(MATRIX_SIZE)] 
 
				# 染色体个数，即总群数量
        self.genes: Set[Gene] = set() 

初始化种群

初始化完参数以后，接下来就需要对种群进行初始化：

class GA:
  	# 初始化种群 [0, 1, 2, 1, 2, 0, 0, 1] => 12
    def init_population(self):
        for _ in range(self.population_size):
            # step1：初始化染色体
            g = Gene() 
            size = self.process_number * self.resource_number
            index_list = list(range(size))
            
            chromosome = [-1 for _ in range(size)]
            for j in range(self.process_number):
                for k in range(self.resource_number):
                    index = randint(0, len(index_list) - 1)
                    val = index_list.pop(index)

                    # self.task_matrix[j][k]表示第j个顺序编号的流程在第k个顺序编号的资源上的任务编号
                    if self.task_matrix[j][k] != -1:
                        chromosome[val] = j 
            g.chromosome = list(filter(lambda x: x != -1, chromosome)) #移除染色体chromosome中无效的成员-1
            
            # step2：计算染色体的适应度
            g.fitness = self.get_fitness(g)
            
            # step3：染色体添加到种群
            self.genes.add(g)

适应度评估

前面初始化种群时，要计算每个染色体的适应度，如下是染色体适应度的计算，在计算前，需要将染色体解码成实际的问题，用实际的问题来评估适应度。

这里我们是执行总耗时多少来评估适应度，执行越耗时，则适应度越低，呈倒数关系。

# 存储解码结果
class GeneEvaluation:
    def __init__(self):
        self.fulfill_time = 0
        self.resource_work_time = [0 for _ in range(MATRIX_SIZE)]
        self.task_ids = [0 for _ in range(MATRIX_SIZE)]
        self.end_time = [[0 for _ in range(MATRIX_SIZE)] for _ in range(MATRIX_SIZE)]
        self.start_time = [[0 for _ in range(MATRIX_SIZE)] for _ in range(MATRIX_SIZE)]

class GA:
    # 适应度评估
    def get_fitness(self, g: Gene) -> float:
        '''
        执行总耗时越多，适应度越低，是倒数关系
        '''
        return 1 / self.translate_gene(g).fulfill_time
    
    # 计算当前染色体的执行总耗时
    def translate_gene(self, g: Gene) -> GeneEvaluation:
        '''
        计算当前染色体的执行总耗时
        '''
        evaluation = GeneEvaluation()
        for process_seq_id in g.chromosome:
            # process_seq_id表示流程的顺序编号
            # task_seq_id表示任务的顺序编号
            # resource_seq_id表示资源的顺序编号
            # resource_work_time表示当前资源处理所处的时间
            
            '''
            当前process_seq_id个流程是第task_seq_id个任务。
            计算某个流程的第一个任务时，task_seq_id=0，
            计算某个流程的第二个任务时，task_seq_id=1，即依次自增长处理
            '''
            task_seq_id = evaluation.task_ids[process_seq_id]
            resource_seq_id = self.resource_matrix[process_seq_id][task_seq_id] # 第process_seq_id个流程第task_seq_id个任务所使用的资源编号
            time = self.time_matrix[process_seq_id][task_seq_id] # 第process_seq_id个流程第task_seq_id个任务所用的执行时间
            evaluation.task_ids[process_seq_id] += 1 # 下次处理process_seq_id流程的第task_seq_id+1个任务
            if task_seq_id == 0:
                evaluation.start_time[process_seq_id][task_seq_id] = evaluation.resource_work_time[resource_seq_id]
            else:
                evaluation.start_time[process_seq_id][task_seq_id] = max(evaluation.end_time[process_seq_id][task_seq_id - 1],
                                            evaluation.resource_work_time[resource_seq_id])
            # resource_work_time其实是资源resource_seq_id执行的结束时间
            evaluation.resource_work_time[resource_seq_id] = evaluation.start_time[process_seq_id][task_seq_id] + time
            evaluation.end_time[process_seq_id][task_seq_id] = evaluation.resource_work_time[resource_seq_id]
            # 最后一个资源执行结束的时间就是当前染色体的执行总耗时
            evaluation.fulfill_time = max(evaluation.fulfill_time, evaluation.resource_work_time[resource_seq_id])
        return evaluation

下面的代码片段，即第process_seq_id个流程的task_seq_id任务开始时间，取其上一个task_seq_id-1任务的结束时间和资源resource_id当前所处的时间的最大值

evaluation.start_time[process_seq_id][task_seq_id] = max(evaluation.end_time[process_seq_id][task_seq_id - 1],
                                            evaluation.resource_work_time[resource_seq_id])

例如下面，当前正在计算#T-02-01任务的开始时间，则由于#T-02-01在资源#R-10001上执行，而当前资源#R-10001所处时间是刚执行完#T-00-01（即evaluation.resource_work_time[resource_seq_id]），而#T-02-01的上一个任务#T-02-00结束时间较小，所以#T-02-01得开始时间应该取evaluation.resource_work_time[resource_seq_id]。

如下，如果当前处理的任务#T-02-01，其上一个任务#T-02-00的结束时间比当前资源evaluation.resource_work_time[resource_seq_id]所在时间大，则这是必须等上一个任务执行结束后才开始执行#T-02-01，也就是任务#T-02-01的开始时间取值为上一个任务#T-02-00的结束时间。

初始化完种群以后，接下来就需要对种群进行交叉繁衍，即先选择两个父母染色体进行交叉繁衍，这里涉及到select和crossover两个操作。

选择

选择（select）操作是根据个体适应度对种群进行筛选，以便优秀的个体有更多的机会进行繁殖。以下是一些常用的遗传算法选择方法：

1. 轮盘赌选择：根据个体适应度占总适应度的比例来分配选择概率。适应度较高的个体被选择的概率较大，适应度较低的个体被选择的概率较小。
2. 锦标赛选择：从种群中随机选取一定数量的个体，然后选择其中适应度最高的个体。这个过程重复进行，直到选择出足够数量的个体。
3. 排序选择：按照个体的适应度对种群进行排序，然后根据排名分配选择概率。适应度排名靠前的个体被选择的概率较大，适应度排名靠后的个体被选择的概率较小。
4. 指数选择：与排序选择类似，但是在分配选择概率时采用指数函数，使得适应度较高的个体被选择的概率更大。
5. 随机普遍选择：在轮盘赌选择的基础上，采用等间隔的方式选择个体，可以保证选择过程更加公平。
6. 标定选择：直接选择适应度排名靠前的一部分个体，舍弃适应度较低的个体。这种方法选择压力较大，可能导致早熟收敛。
7. 线性标定选择：与排序选择类似，但是在分配选择概率时采用线性函数，使得适应度较高的个体被选择的概率更大。

这里我们采用锦标赛方法。

class GA:
		# 选择
    def select(self, n: int = 3):
        '''
        在锦标赛选择中，从种群中随机采样n个个体，然后选择最优的个体进入下一代，只有个体的适应度值优于其他n-1个竞争者时才能赢得锦标赛。所以，这里最差的个体永远不会幸存，而最优的个体在其参与的所有锦标赛中都能获胜。
        '''
        index_list = list(range(len(self.genes)))
        index_set = {index_list.pop(randint(0, len(index_list) - 1)) for _ in range(n)}
        best_gene = Gene(0)
        i = 0
        for gene in self.genes:
            if i in index_set:
                if best_gene.fitness < gene.fitness:
                    best_gene = gene
            i += 1
        return best_gene

交叉

选出两个优秀的父母个体以后，接下来就进行交叉染色体进行繁衍：

class GA:
		# 交叉
    def crossover(self, g1: Gene, g2: Gene) -> tuple:
        chromosome_size = self.chromosome_size
 
        def gene_generate(father: Gene, mother: Gene) -> Gene:
            # step1:首先随机产生一个起始位置start和终止位置end
            index_list = list(range(chromosome_size))
            p1 = index_list.pop(randint(0, len(index_list) - 1))
            p2 = index_list.pop(randint(0, len(index_list) - 1))
            start = min(p1, p2)
            end = max(p1, p2)

            # step2:并由从father的染色体序列从start到end的序列中产生一个子代原型
            prototype = father.chromosome[start: end + 1]

            # step3:将mother中不包含在child prototype的其余编码加入到child prototype两侧
            t = mother.chromosome[0:]
            for v1 in prototype:
                for i in range(len(t)):
                    if v1 == t[i]:
                        t.pop(i)
                        break
            child = Gene()
            child.chromosome = t[0: start] + prototype + t[start:]
            child.fitness = self.get_fitness(child)
            return child
 
        return gene_generate(g1, g2), gene_generate(g2, g1)

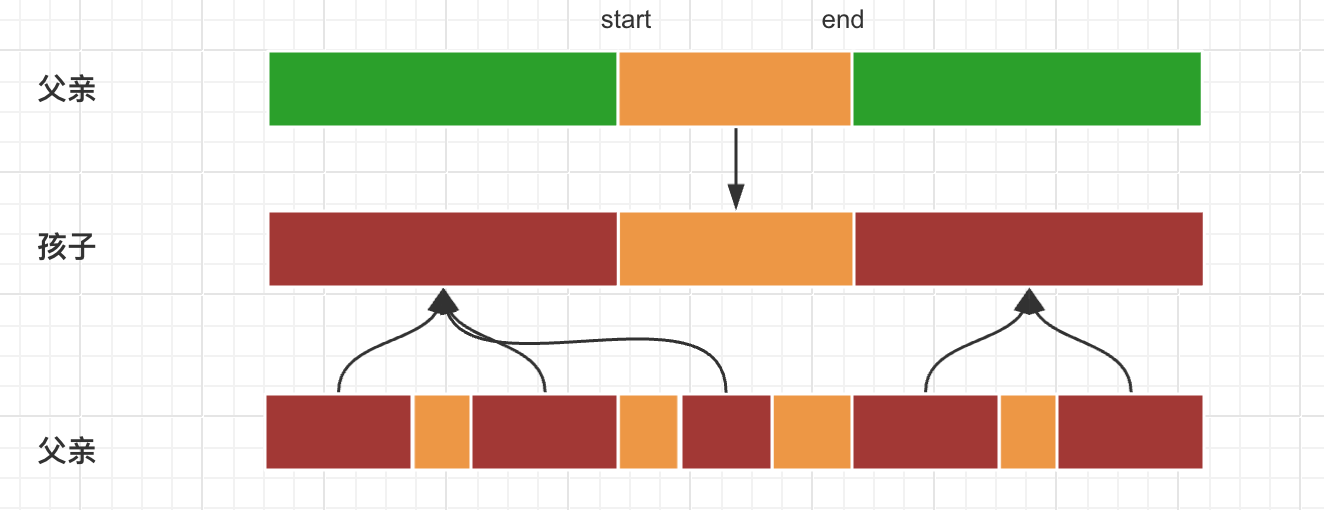
变异

在这里，我们从染色体中随机选择两个位置选择进行交换来模拟变异行为。

class GA:
		# 变异
    def mutate(self, g: Gene, n = 2) -> None:
        index_list = [i for i in range(self.chromosome_size)]
        # 从染色体中随机产生两个位置并交换这两个位置的值
        for i in range(n):
            a = index_list.pop(randint(0, len(index_list) - 1))
            b = index_list.pop(randint(0, len(index_list) - 1))
            g.chromosome[a], g.chromosome[b] = g.chromosome[b], g.chromosome[a]
 
        g.fitness = self.get_fitness(g)

主函数

run函数是GA类的调用入口：

class GA:
		def run(self, parameter: List[List[Tuple]]) -> GeneEvaluation:
        '''
        例如： parameter==> [
            [(0, 5)], 
            [(3, 10), (2, 21), (4, 12)], 
            [(3, 10), (0, 11), (2, 5)], 
            [(1, 21), (3, 21)]
        ]
        parameter就是ans二维数组
        '''
        process_size = len(parameter)
        for i in range(process_size):
            # parameter[i]表示任务数组，记录了每个任务在资源上的执行耗时，即（资源顺序编号，执行耗时）
            self.chromosome_size += len(parameter[i]) # 所有任务的数量就是染色体大小
            # 取所有流程里面任务数量最多的作为最大值
            self.task_number = max(self.task_number, len(parameter[i])) 
            for j in range(len(parameter[i])):
              	# self.resource_matrix[i][j]表示第i个流程的第j个任务的资源顺序编号
                self.resource_matrix[i][j] = parameter[i][j][0] 
                # self.time_matrix[i][j]表示第i个流程的第j个任务所在资源的执行耗时
                self.time_matrix[i][j] = parameter[i][j][1] 
 
        for i in range(process_size):
            for j in range(self.task_number):
                if self.resource_matrix[i][j] != -1:
            				# i表示第i个流程，j表示第j个任务，self.resource_matrix[i][j]表示资源的顺序编号
              			# 则task_matrix表示在第i个顺序流程，第x个资源上的任务顺序编号
                    self.task_matrix[i][self.resource_matrix[i][j]] = j 
 
        self.init_population()
 
        for _ in range(self.times):
            probability = randint(1, 100) / 100
            # 控制变异概率
            if probability < self.mutation_rate:
                index = randint(0, len(self.genes))
                i = 0
                for gene in self.genes:
                    if i == index:
                        self.mutate(gene) # 变异
                        break
                    i += 1
            else:
                g1, g2 = self.select(), self.select()
                children = self.crossover(g1, g2)
                self.genes.update({*children}) # 修改总群染色体，新染色体则添加，重复则忽略。
 
        best_gene = Gene(0)
        for gene in self.genes:
            if best_gene.fitness < gene.fitness:
                best_gene = gene
 
        return self.translate_gene(best_gene) # 解码

调度函数，其中ResultData用于存储执行的结果。其中fulfill_time是遗传算法返回的最终执行耗时，row_data返回了每个任务在哪个资源以及什么时候执行，gant_data返回以资源视角的甘特图。

ResultData = namedtuple("ResultData", ["fulfill_time", "row_data", "gant_data"])
 
# 输出结果
def schedule(data) -> ResultData:
    reshape = reshape_data(data)
    parameter = reshape.result
    n = len(reshape.process)
    m = len(reshape.resource)  # number from 0
    ga = GA(process_number = n, resource_number = m)
    result = ga.run(parameter)
    p = ga.task_number
    resource_matrix = ga.resource_matrix
    row_data = []
    for i in range(n):
        for j in range(p):
            if resource_matrix[i][j] != -1:
                temp = {
                    "process": reshape.process[i],
                    "task": reshape.task[i][j],
                    "resource": reshape.resource[resource_matrix[i][j]],
                    "startTime": result.start_time[i][j],
                    "endTime": result.end_time[i][j]
                }
                row_data.append(temp)
 
    gant_data = {}
    for i in range(n):
        for j in range(p):
            if resource_matrix[i][j] != -1:
                temp = {
                    "process": reshape.process[i],
                    "task": reshape.task[i][j],
                    "startTime": result.start_time[i][j],
                    "endTime": result.end_time[i][j]
                }
                m = reshape.resource[resource_matrix[i][j]]
                if m not in gant_data:
                    gant_data[m] = [temp]
                else:
                    gant_data[m].append(temp)
    return ResultData(result.fulfill_time, row_data, gant_data)

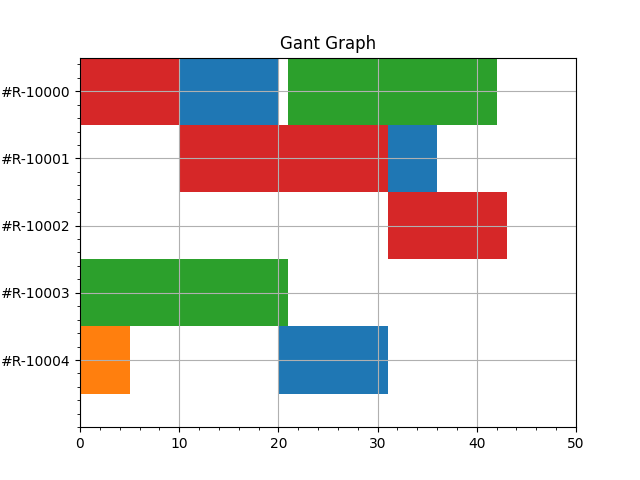
为了更好理解生成的调度计划，我们通过甘特图来表示：

# 绘制资源甘特图
def show_gant(gant_data):
    fig, ax = plt.subplots()
    
    ax.set_title('Gant Graph')
    ax.minorticks_on()
    ax.set_ylim(5, 60)
    ax.set_xlim(0, 50)
    
    idx_list = [15,25,35,45,55]
    labels = ['#R-10004', '#R-10003', '#R-10002', '#R-10001', '#R-10000']
    ax.set_yticks(idx_list, labels=labels)
    color = {
        '#P-00': 'red',
        '#P-01': 'green',
        '#P-02': 'blue',
        '#P-03': 'orange',
    }

    y = 0
    for res in labels:
        task_list = gant_data[res]
        y += 10
        xranges = []
        facecolors = []
        for v in task_list:
            length = int(v['endTime']) - int(v['startTime'])
            xranges.append( (v['startTime'], length) )
            facecolors.append( 'tab:{}'.format(color[v['process']]) )
        ax.broken_barh(xranges, (y, 10), facecolors=tuple(facecolors))
    
    
    plt.grid()
    plt.show()

下面，我们以前面的3个流程进行测试：

if __name__ == "__main__":
    # 测试数据
    data = [{'process': '#P-00', 'task': '#T-00-00', 'resource': '#R-10000', 'time': 10, 'order': 0},
         {'process': '#P-00', 'task': '#T-00-01', 'resource': '#R-10001', 'time': 21, 'order': 1},
         {'process': '#P-00', 'task': '#T-00-02', 'resource': '#R-10002', 'time': 12, 'order': 2},

         {'process': '#P-01', 'task': '#T-01-00', 'resource': '#R-10003', 'time': 21, 'order': 0},
         {'process': '#P-01', 'task': '#T-01-01', 'resource': '#R-10000', 'time': 21, 'order': 1},

         {'process': '#P-02', 'task': '#T-02-02', 'resource': '#R-10001', 'time': 5, 'order': 2},
         {'process': '#P-02', 'task': '#T-02-01', 'resource': '#R-10004', 'time': 11, 'order': 1},
         {'process': '#P-02', 'task': '#T-02-00', 'resource': '#R-10000', 'time': 10, 'order': 0},

         {'process': '#P-03', 'task': '#T-03-00', 'resource': '#R-10004', 'time': 5, 'order': 0}]
    resultData = schedule(data)
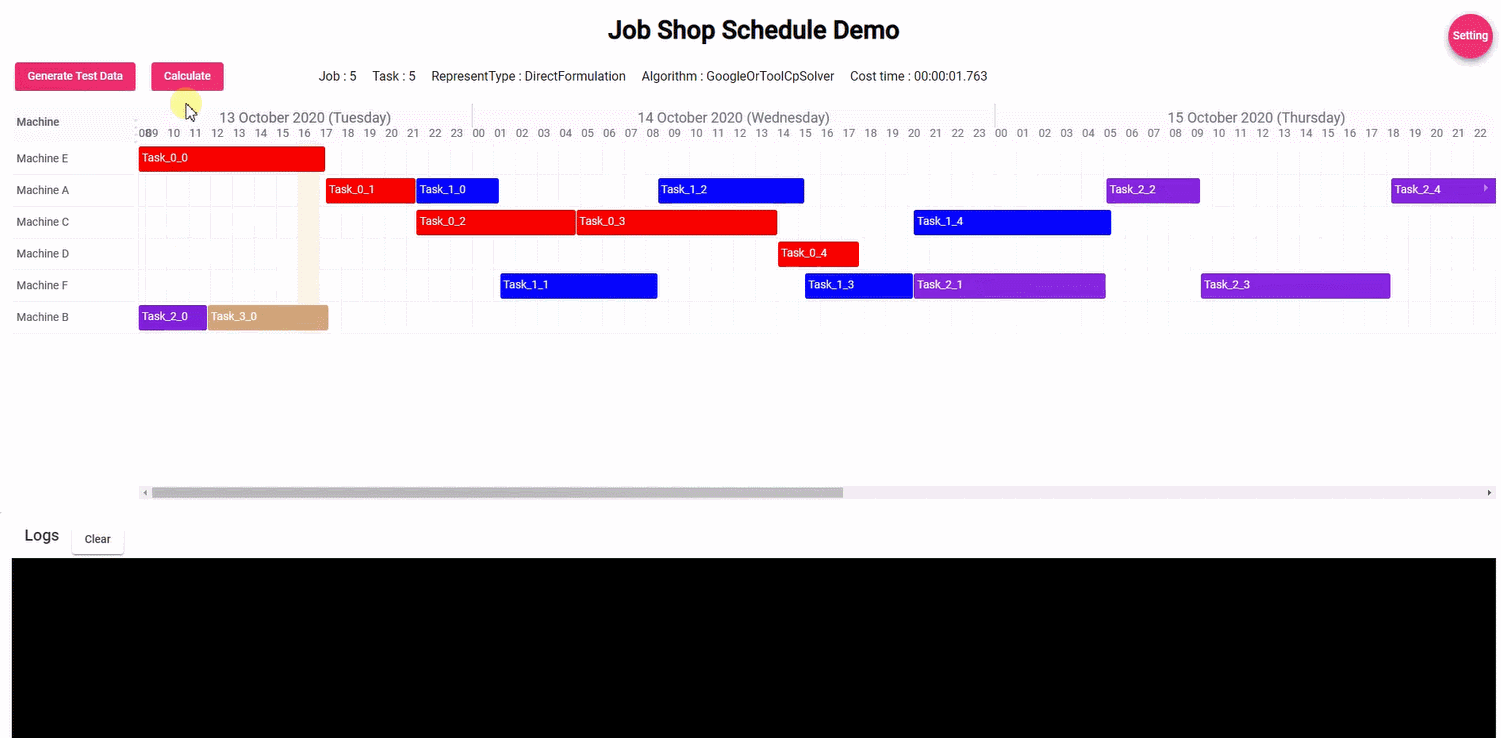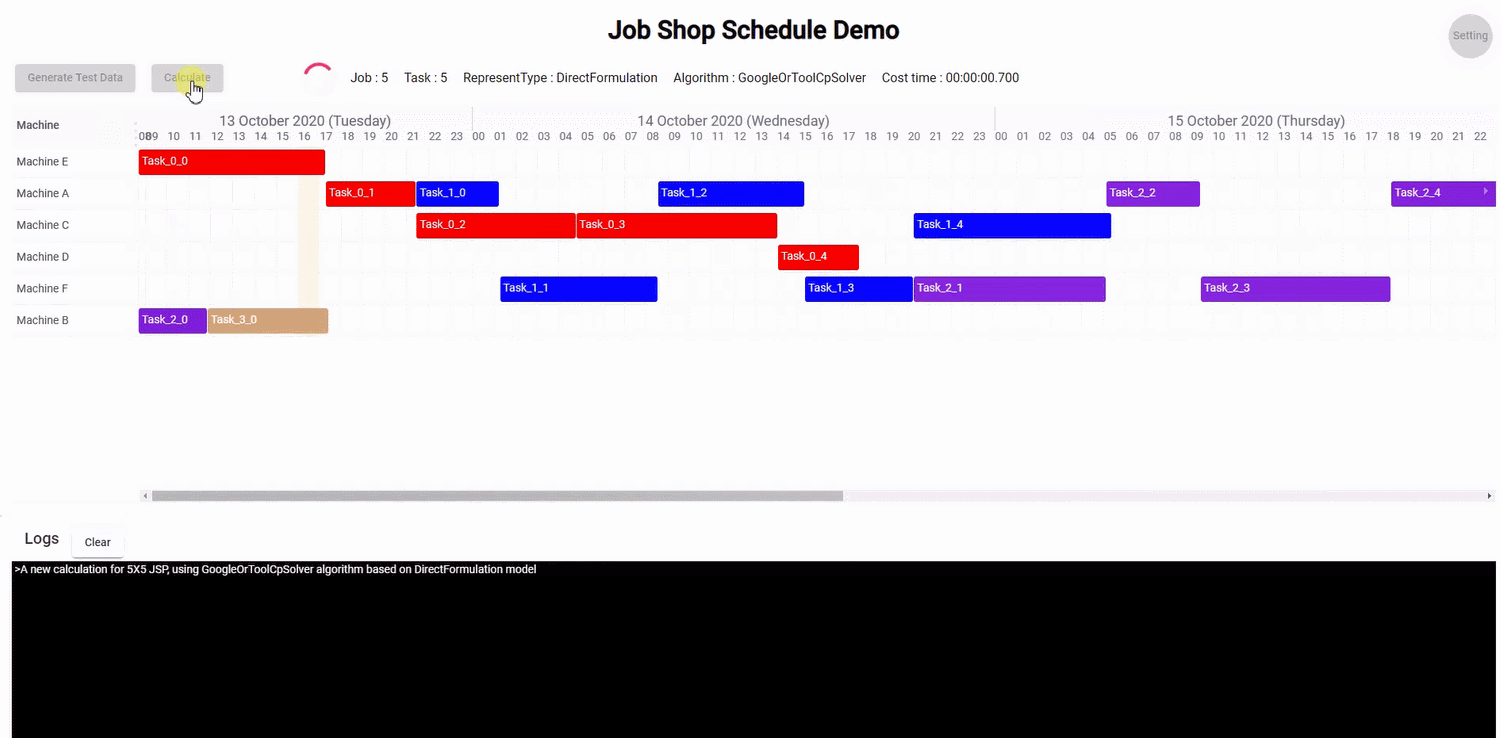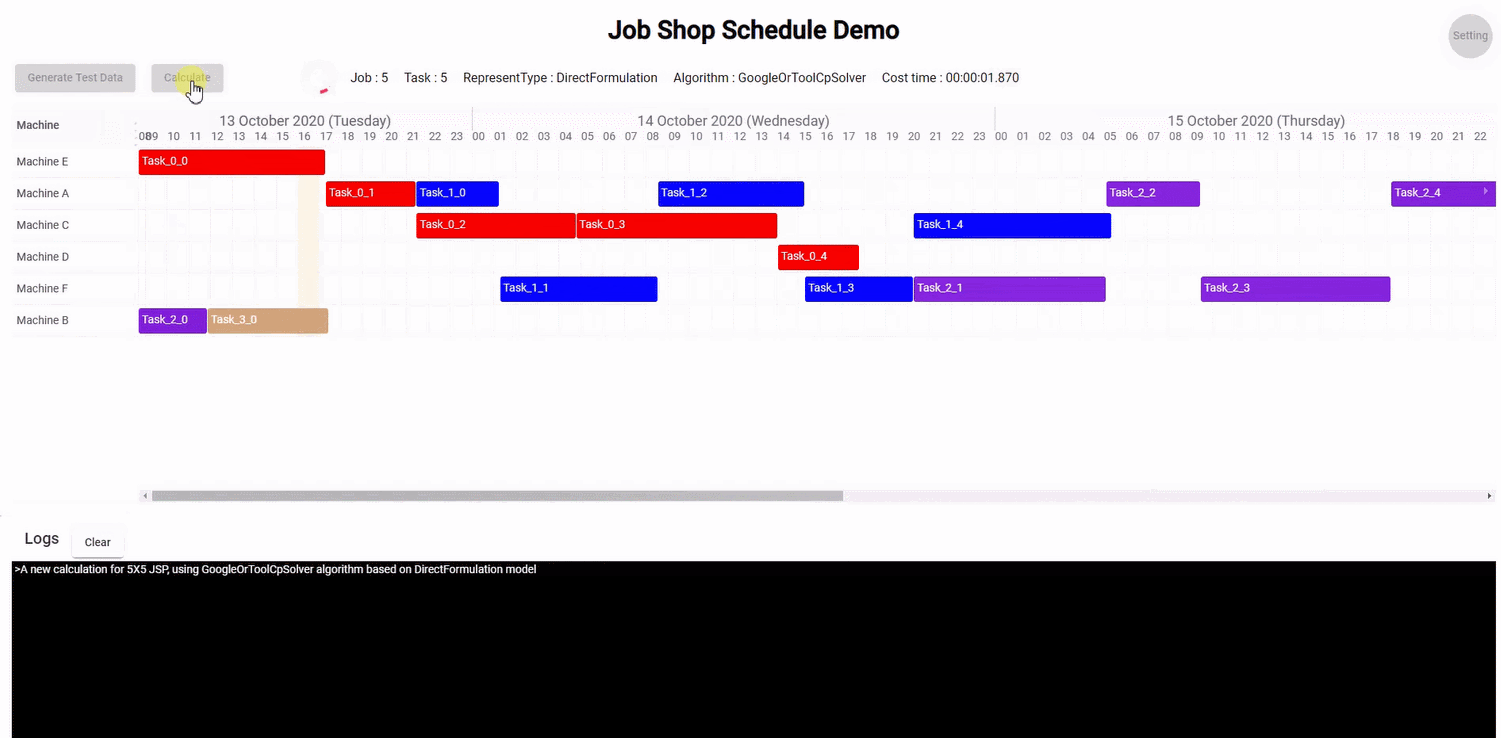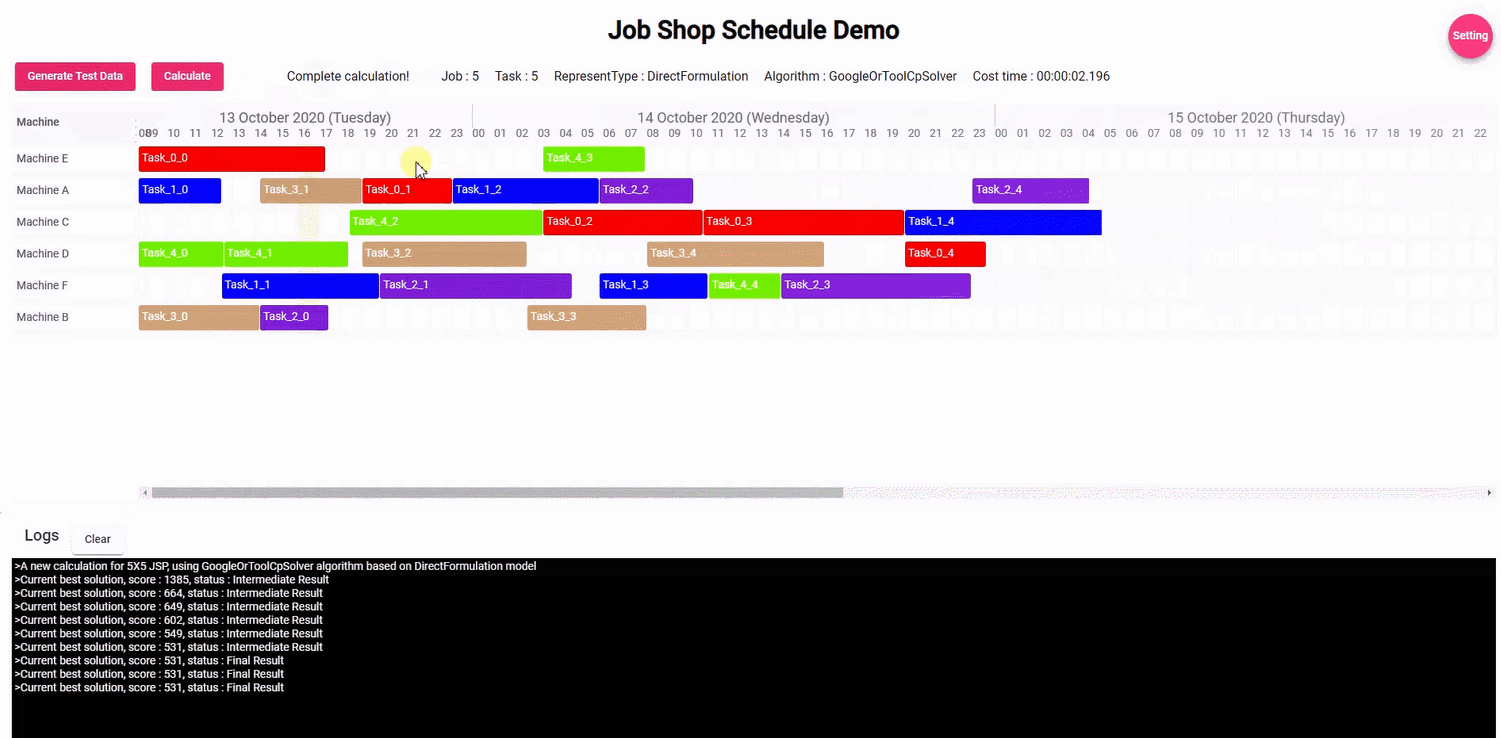
    print('fulfill_time==>',resultData.fulfill_time)
    print('row_data==>',json.dumps(resultData.row_data))
    print('gant_data==>',json.dumps(resultData.gant_data)) # 资源甘特图

    show_gant(resultData.gant_data)

下面是运行的结果：

蚁群算法

待补充

粒子群算法

待补充

模拟退火算法

待补充