流程引擎原理与实践

# 基本概念介绍

在我们具体展开流程引擎的各种实现方法之前，有必要先交代下这些流程引擎实现过程中涉及到的一些基础技术和概念。

# 拓扑排序

拓扑排序是针对有向图（Directed Graph）的一种排序方法，它将有向图中的顶点以线性顺序进行排序，满足以下条件：对于图中的每条有向边 (u, v)，在排序后的序列中，顶点 u 必须排在顶点 v 的前面。

拓扑排序仅适用于有向无环图（DAG），即不存在环路的有向图。这是因为如果图中存在环路，就会导致无法进行拓扑排序，因为无法找到满足上述条件的排序顺序。

实现方法

拓扑排序可以通过深度优先搜索（DFS）或广度优先搜索（BFS）来实现。基本思路是从图中选择一个没有入边的顶点（即入度为 0 的顶点）作为排序的起点，然后从图中移除与该顶点相连的边，继续寻找没有入边的顶点。这个过程一直持续下去，直到所有的顶点都被排序。

应用

拓扑排序在实际中有许多应用，尤其在计算机科学和工程领域中是非常重要的：

  1. 任务调度： 在工程和计算任务中，拓扑排序能够有效地确定任务执行的顺序，特别是在有依赖关系的情况下。

  2. 编译器优化： 在编译器中，拓扑排序有助于确定源代码中各个模块之间的依赖关系，从而优化编译过程的顺序。

  3. 数据流分析： 在静态分析中，拓扑排序用于确定数据流分析的顺序，以便有效地分析变量之间的依赖关系。

  4. 依赖关系分析： 许多系统和任务之间存在依赖关系，拓扑排序有助于分析这些依赖关系，并确定执行或处理的顺序。

拓扑排序是一种强大的算法技术，能够帮助处理各种问题中的顺序性和依赖关系，并提供一种有序的处理方式。

下面我们对拓展排序的两种实现方法，深度优先搜索和广度优先搜索进行简单的介绍，尤其是广度优先算法（BFS）会作为基于DAG方式实现流程引擎的核心图遍历算法。

# 广度优先算法（BFS）

广度优先搜索（Breadth-First Search，BFS）是一种图遍历算法，用于遍历或搜索图中的节点。它从一个指定的节点开始，首先访问该节点的所有邻居节点，然后依次访问这些邻居节点的邻居节点，以此类推，直到遍历完整个连通区域。

BFS 通常使用队列来实现。

算法步骤

  1. 选择一个起始节点，将其标记为已访问，并将其加入队列中。
  2. 从队列中取出一个节点，访问它的所有未标记邻居节点，并将这些邻居节点标记为已访问，并加入队列。
  3. 重复步骤 2，直到队列为空为止。

BFS 的特点是按层级逐步扩展，首先遍历起始节点的所有直接邻居，然后是邻居的邻居，以此类推，直到遍历完整个。

伪代码实现

输入：图Graph和它的根节点start_node

输出：遍历图Graph

BFS(Graph, start_node):
    queue = empty queue  // 这里使用到队列的数据结构
    visited = set() 

    add start_node to queue
    mark start_node as visited

    while queue is not empty:
        current_node = queue.dequeue()
        print current_node

        for each neighbor in Graph.adjacentNodes(current_node):
            if neighbor is not in visited:
                add neighbor to queue
                mark neighbor as visited

这段伪代码描述了 BFS 算法的基本逻辑：

  1. 从指定的起始节点开始。
  2. 使用一个队列(FIFO)存储待访问的节点，并使用一个集合（可以是哈希集）来标记已经访问过的节点。
  3. 将起始节点加入队列，标记为已访问。
  4. 当队列不为空时，循环执行以下操作：
    • 取出队列中的当前节点。
    • 访问并处理当前节点。
    • 遍历当前节点的邻居节点：
      • 如果邻居节点尚未被访问，将其加入队列，并标记为已访问。

请注意，伪代码中的 Graph.adjacentNodes(current_node) 表示获取当前节点的邻居节点列表。

举例说明

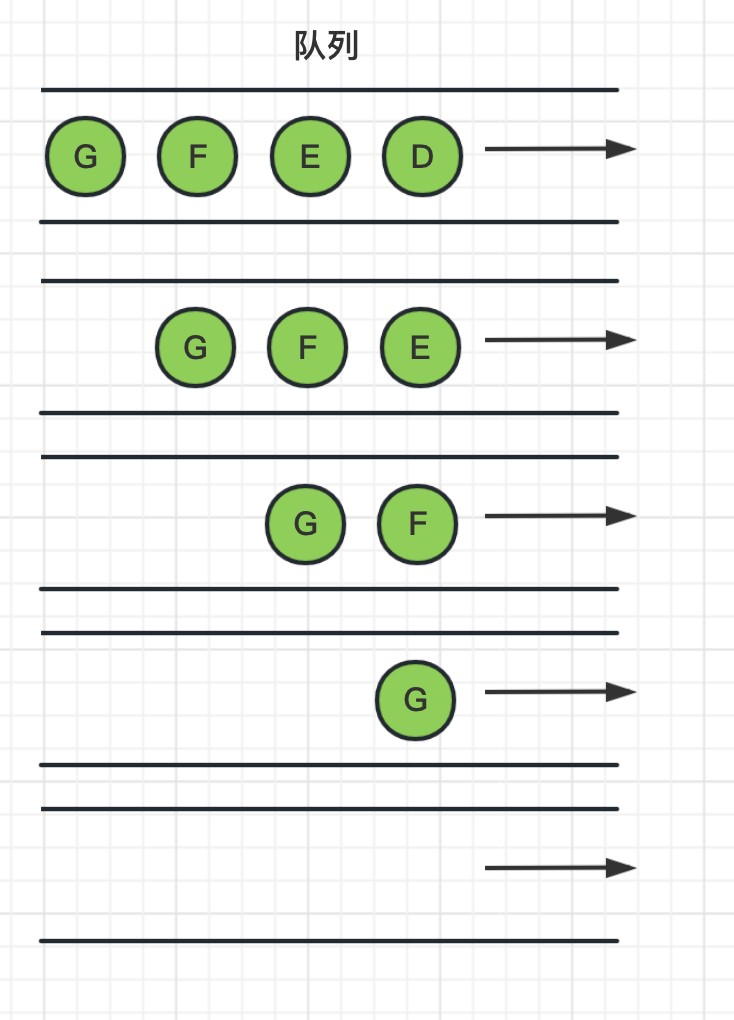
1、首先将起始节点A推送到队列中，并将节点A表示为已访问

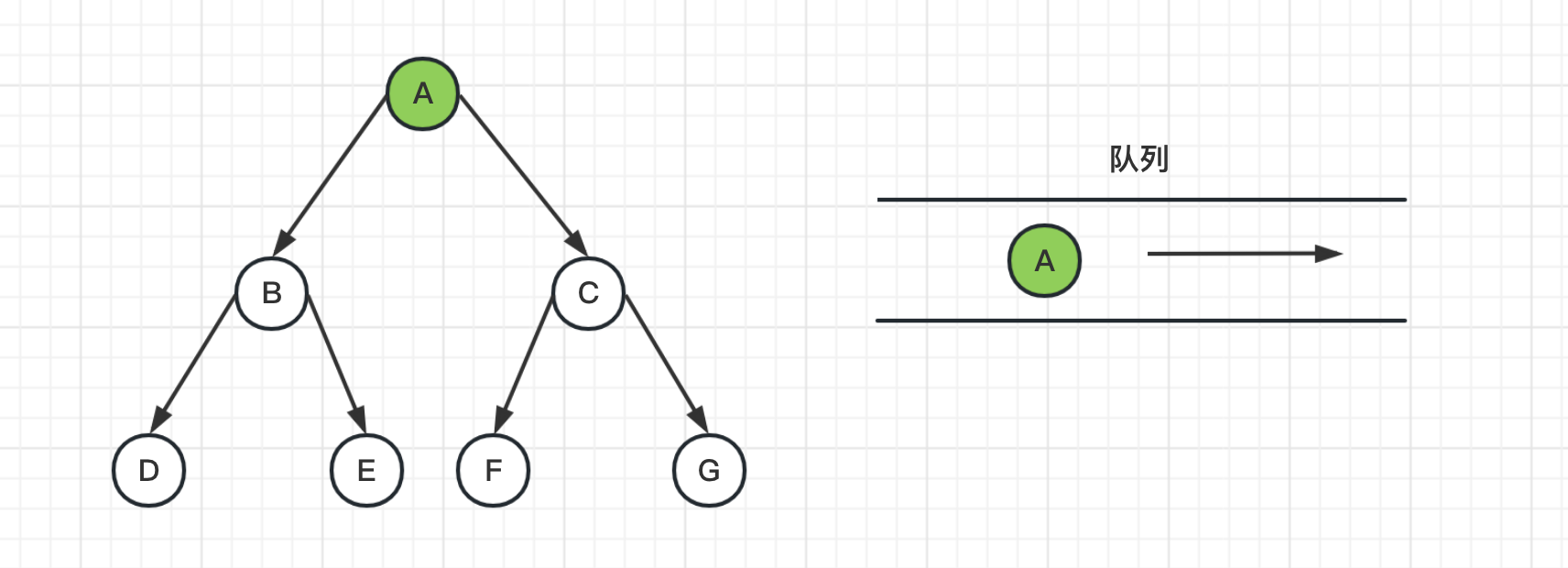
image-20231030235734431

2、从队列头中取出节点A，并获取其邻居节点BC，把BC节点推送到队列，并标记为已访问

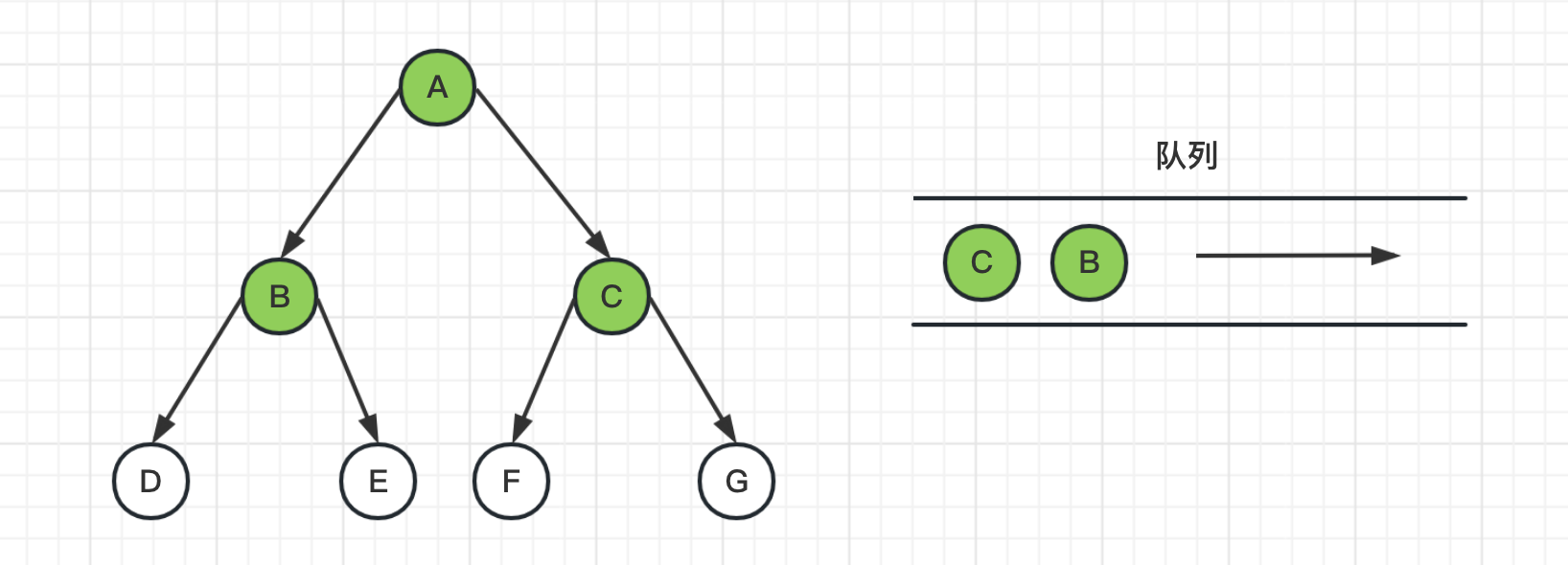
image-20231031000040786

3、从队列头中取出节点B，并获取其邻居节点DE，把DE节点推送到队列，并标记为已访问

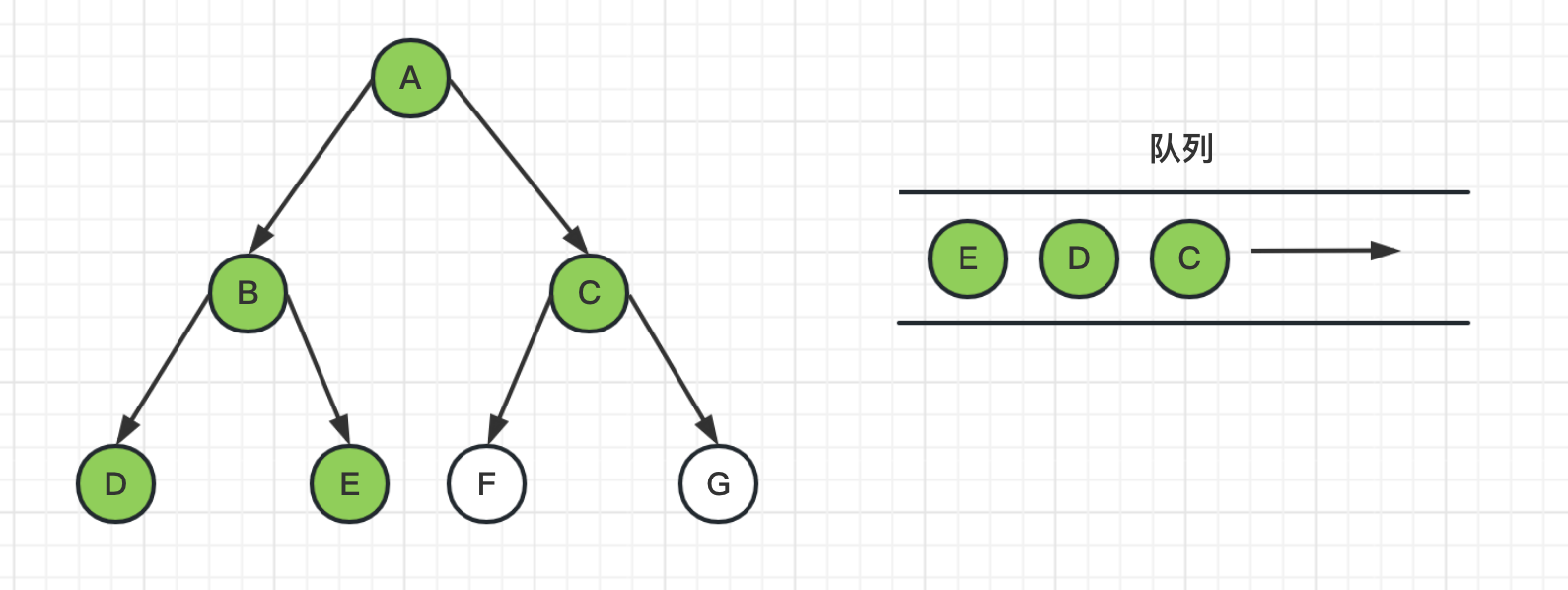
image-20231031000241471

4、从队列头中取出节点C，并获取其邻居节点FG，把FG节点推送到队列，并标记为已访问

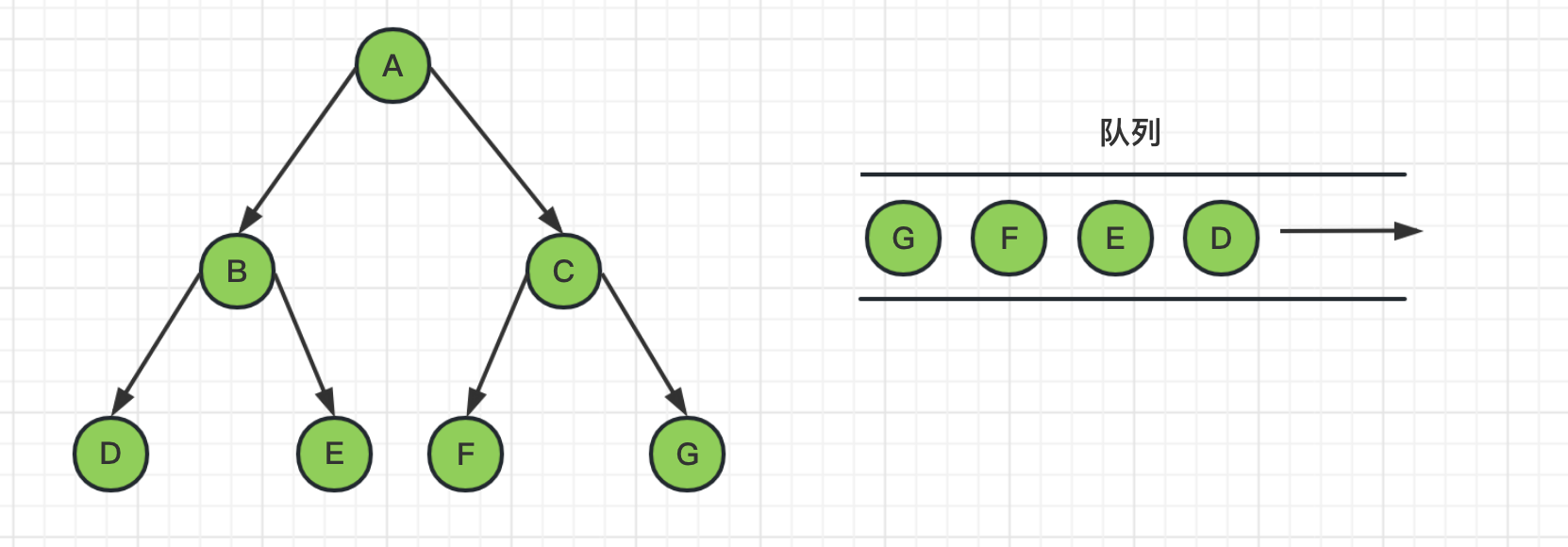
image-20231031000429387

5、然后继续从队列头中，依次把D、E、F、G节点取出来，由于DEFG都是叶子节点没有邻居节点，所以就没有入队列的操作。最后队列为空，图遍历结束。

image-20231031000642558

应用

  • 最短路径和最小操作问题： 在无权图中，BFS 可以用于查找节点 A 到节点 B 的最短路径。在这种情况下，BFS 从起始节点开始，逐层遍历直到找到目标节点。这同样适用于网络中数据包的传输路径、社交网络中的最短关系链等。

  • 解决谜题和游戏： BFS 可用于解决一些谜题，例如迷宫问题或寻找棋盘游戏中的最优解。通过逐层搜索可能的路径，可以找到解决方案或最优解。

  • 网络广播和社交网络分析： 在计算机网络中，BFS 可用于广播信息或寻找特定信息的传播路径。在社交网络分析中，BFS 可用于查找特定节点的关联节点，以及发现社交网络中的群体或子网络。

  • 拓扑排序： BFS 可用于拓扑排序，在有向图中对节点进行排序，以便进行有序处理或执行。

  • 检测环路： BFS 在检测图中是否存在环路时也很有用。在搜索过程中，若发现某节点的邻居节点已经被访问但并非其父节点，说明图中存在环路。

这些只是广度优先搜索在实际应用中的一些典型场景。BFS 作为一种重要的图遍历算法，被广泛应用于网络路由、数据检索、图论、计算机科学和各种领域的问题求解。

# 深度优先算法（DFS）

深度优先搜索（Depth-First Search，DFS）也是一种用于遍历或搜索图的算法。DFS 从起始节点开始，沿着一条路径尽可能深地遍历完这条路径，直到到达最深的节点，然后回溯并探索其他路径。

算法步骤

  1. 从指定起始节点开始递归或使用栈的方式遍历与其相邻的节点。
  2. 对于每个相邻节点，若该节点未被访问，则递归或压入栈并访问该节点。
  3. 继续对未被访问的相邻节点进行深度优先搜索。

伪代码实现

输入：图Graph和它的根节点start_node

输出：遍历图Graph

DFS(Graph, start_node):
    stack = empty stack  // 这里使用到栈的数据结构
    visited = set()  // 用来存储已经访问过的节点

    add start_node to stack

    while stack is not empty:
        current_node = stack.pop()

        if current_node is not in visited:
            print current_node
            mark current_node as visited

            for each neighbor in reverse order of Graph.adjacentNodes(current_node):
                if neighbor is not in visited:
                    add neighbor to stack

请注意，伪代码中的 Graph.adjacentNodes(current_node) 表示获取当前节点的邻居节点列表。

上述伪代码演示了典型的迭代式 DFS 实现方式。这里主要使用栈来模拟递归的行为。

主要步骤包括：

  1. 从起始节点开始，将其加入栈。
  2. 当栈不为空时，循环执行以下操作：
    • 弹出栈顶的当前节点。
    • 若当前节点未被访问，则访问并处理该节点，同时标记为已访问。
    • 遍历当前节点的邻居节点，将未被访问的邻居节点加入栈。

通过使用栈的迭代方式，深度优先搜索可以模拟递归的深度探索过程，不仅更符合典型的 DFS 特性，还能有效地遍历图中的节点。

举例说明

1、如下图，首先将图的根节点A入栈

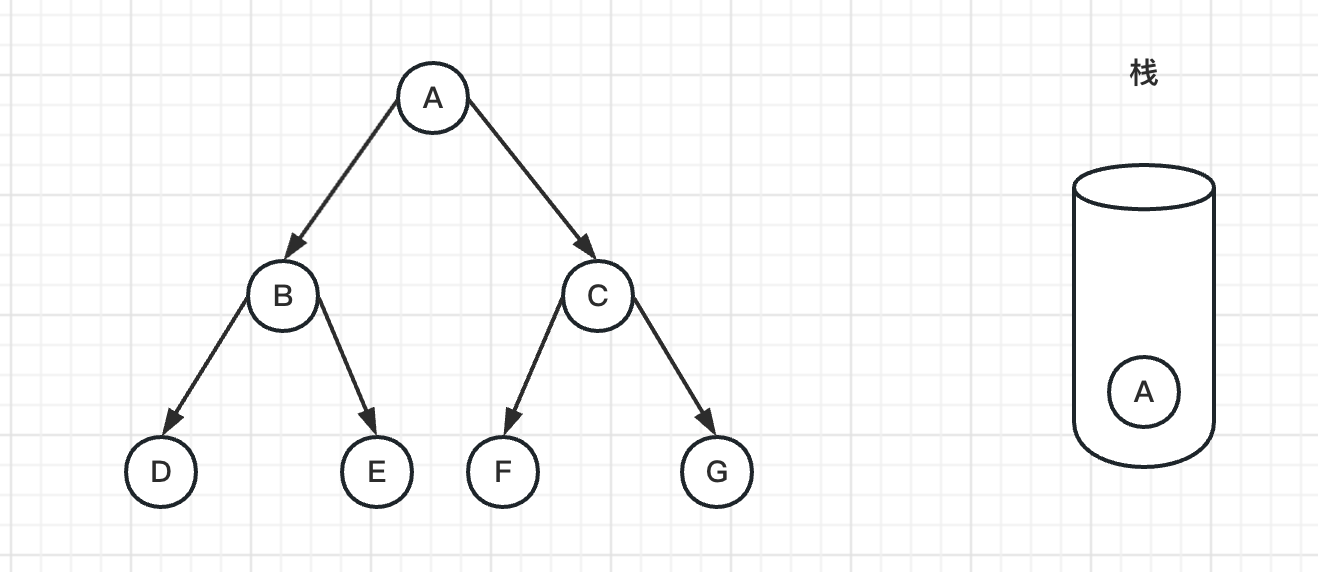
image-20231031091412821

2、然后弹出栈顶节点A，标记A为已访问过，并且把C、B节点入栈

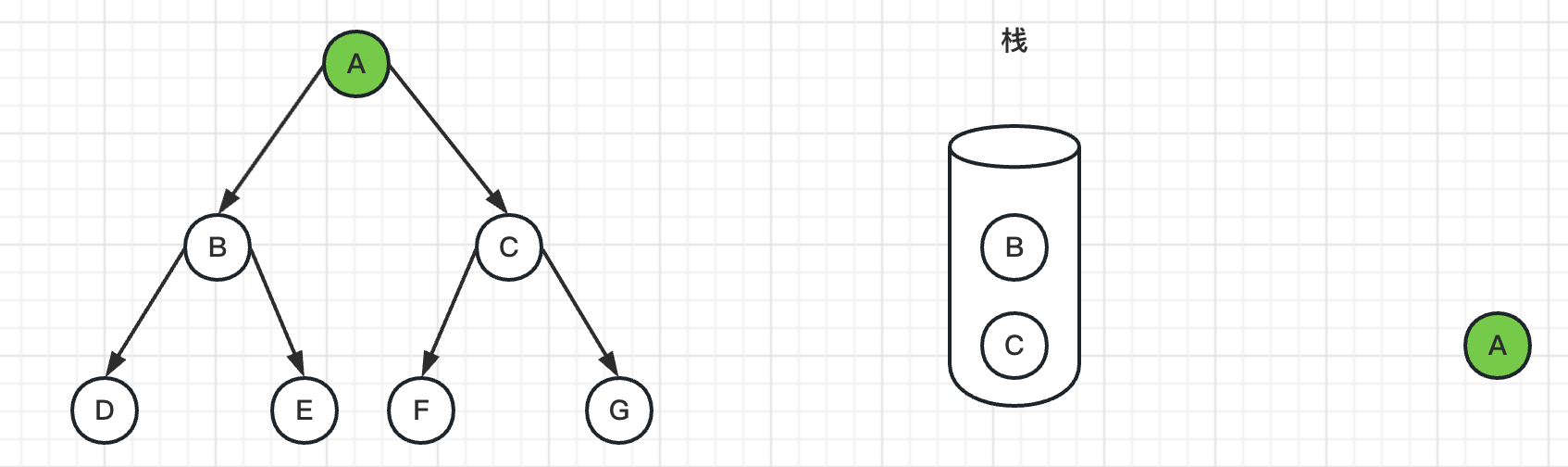
image-20231031091504615

3、弹出栈顶节点B，标记B为已访问过，并且把E、D节点入栈

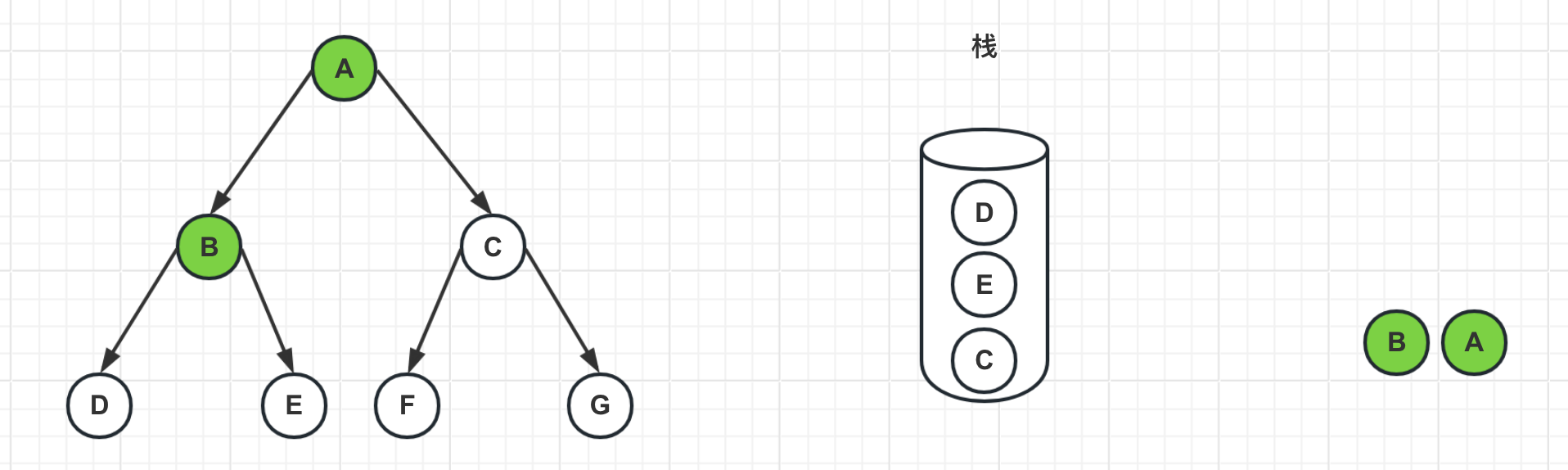
image-20231031091552706

4、弹出栈顶节点D，标记D为已访问过，由于D节点是叶子节点，没有邻居节点，所以没有入栈操作

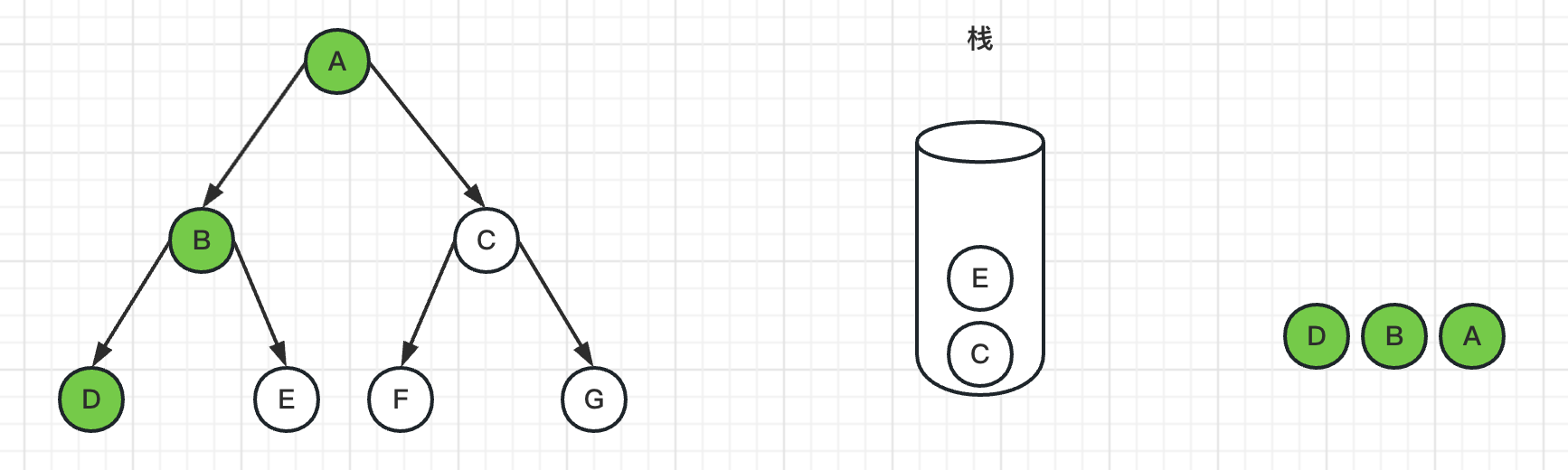
image-20231031091803968

5、弹出栈顶节点E，标记E为已访问过，由于E节点是叶子节点，没有邻居节点，所以没有入栈操作

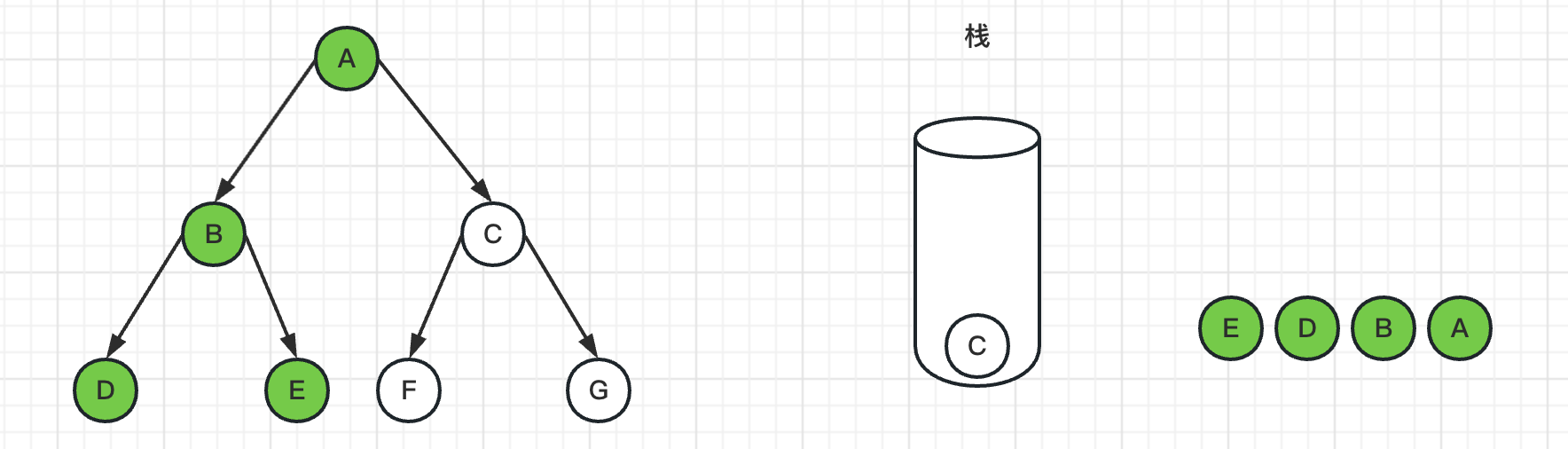
image-20231031091930840

6、弹出栈顶节点C，标记C为已访问过，并且把G、F节点入栈

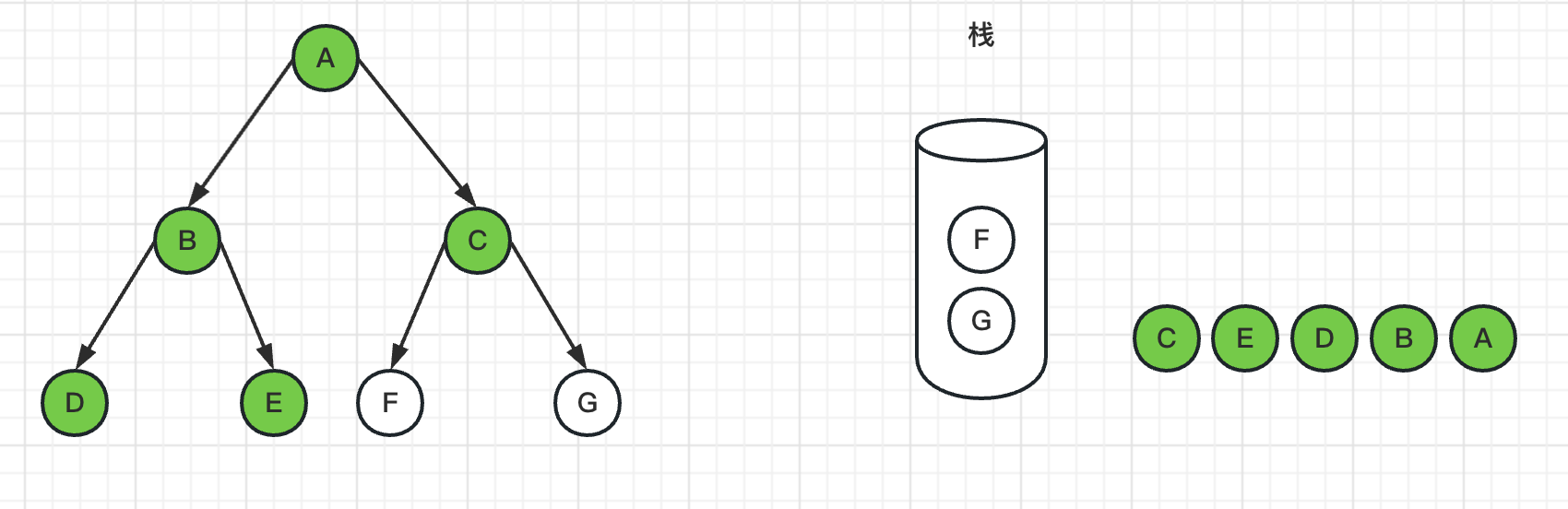
image-20231031092203755

7、弹出栈顶节点F，标记F为已访问过，由于F节点是叶子节点，没有邻居节点，所以没有入栈操作

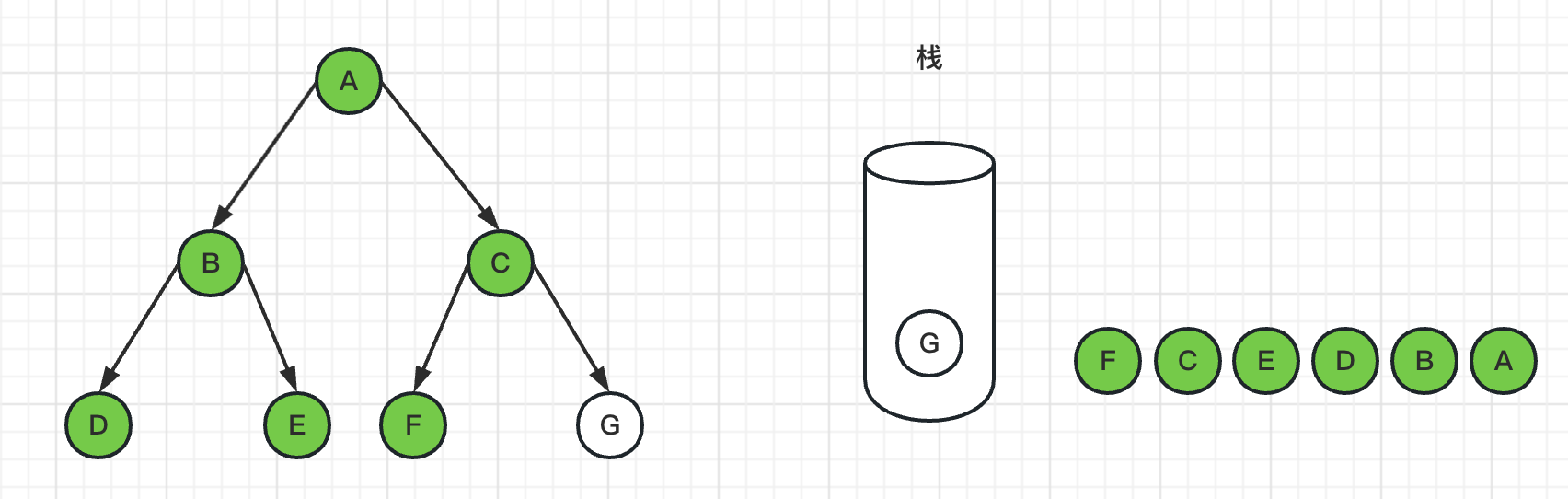
image-20231031092324418

8、弹出栈顶节点G，标记G为已访问过，由于G节点是叶子节点，没有邻居节点，所以没有入栈操作

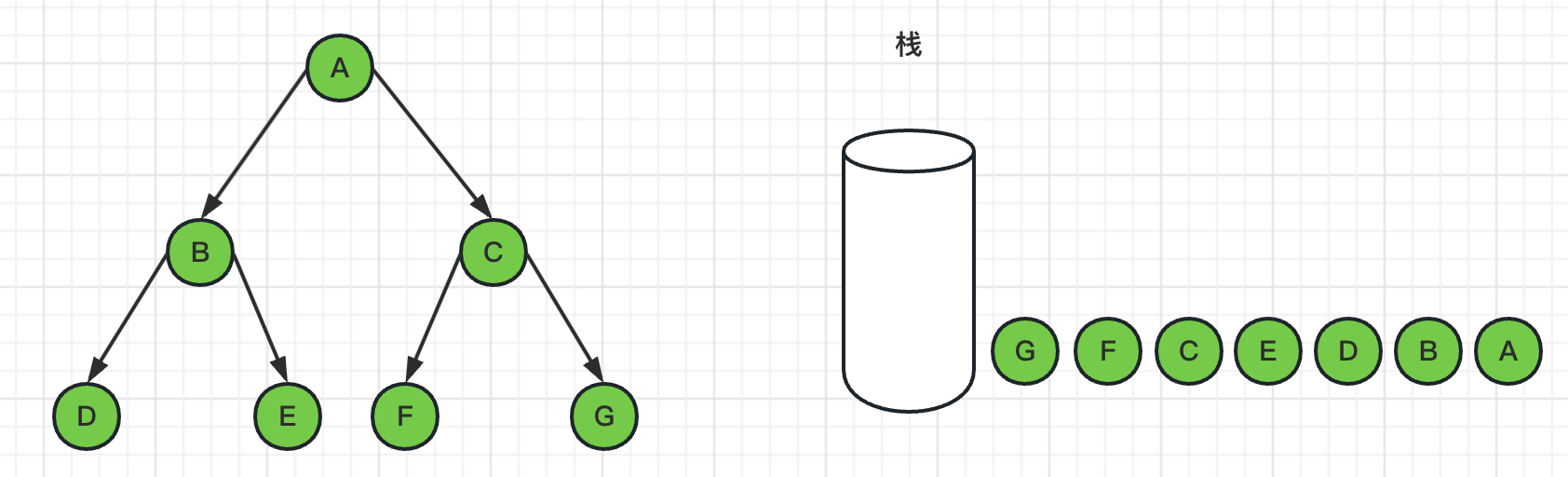
image-20231031092414849

9、此时栈为空，遍历结束

应用

  • 解决路径问题： DFS 通常用于解决路径或连接问题，比如查找图中的路径或寻找连通组件。
  • 拓扑排序： 通过 DFS 可以实现拓扑排序，找出有向无环图中节点的排序序列。
  • 游戏解决： 在游戏设计中，DFS 可用于解决迷宫问题或寻找路径等。

# 基于有向无环图（DAG）的实现

有向无环图（Directed Acyclic Graph，DAG）是图论中的一种特殊类型的图，它由顶点和有向边组成，这些边的方向指示了顶点之间的关系，并且图中不存在环路。

  • 有向边： 每条边都有一个明确的方向，从一个顶点指向另一个顶点。这个方向性表示了顶点之间的关系，例如，如果从顶点 A 到顶点 B 有一条有向边，那么意味着 A 和 B 之间存在某种类型的指向性关系。
  • 无环： 无向无环图中不存在环路，也就是说，无法从一个顶点出发沿着有向边回到该顶点，不论经过多少条边。这使得无向无环图变得特别重要，因为没有环路，从而没有循环依赖或者无限循环的问题，这对于许多算法和数据结构有着重要的意义。

DAG 在计算机科学和相关领域中应用广泛，特别是在任务调度、数据流处理、编译器优化、算法设计等方面。例如，在本书介绍的工作流引擎中，任务之间的依赖关系可以用 DAG 来表示，这有助于有效地安排任务的执行顺序。

基于有向无环图（DAG）的流程引擎是一种使用图论中的有向无环图来描述和管理流程的引擎。在这种设计中，图的顶点表示任务或状态，有向边表示任务或状态之间的依赖关系或顺序关系。

设计思路

  • 顶点表示任务或状态： 每个顶点代表一个特定的任务或状态。例如，任务 A、任务 B、任务 C 等可以是图中的顶点。

  • 有向边表示依赖关系： 有向边表示任务或状态之间的依赖关系。例如，如果任务 A 必须在任务 B 之前执行，则存在从 A 到 B 的有向边。

  • 拓扑排序： 使用拓扑排序算法对有向无环图进行排序，以确定任务或状态的执行顺序。拓扑排序可确保按照图中的依赖关系进行顺序执行。常用广度优先算法或深度优先算法实现。

  • 状态迁移与执行逻辑： 每个任务或状态执行的逻辑与顶点相关联。当确定某个任务或状态处于执行阶段时，执行相应的任务逻辑。

实现流程引擎的步骤

  1. 定义顶点和有向边： 将流程中的任务或状态定义为图的顶点，并确定它们之间的依赖关系。
  2. 构建有向无环图： 基于任务之间的依赖关系构建有向无环图。确保图中不存在循环依赖。
  3. 拓扑排序： 使用拓扑排序算法（这里使用广度优先算法）对图进行排序，以确定任务的执行顺序。这确定了任务或状态的顺序性。
  4. 任务执行与状态切换： 根据拓扑排序的结果执行任务或状态，确保按顺序进行。

基于有向无环图的流程引擎利用图论中的拓扑排序等算法，提供了对任务或状态执行顺序的有效管理和控制。这种方法非常适用于复杂流程的管理和执行。目前主流的Airflow开源软件其核心的引擎调度算法就是基于DAG方式实现。

代码实现

  1. 定义Task类：
class Task:
    def __init__(self, id, name, status, dependencies, actions):
        self.id = id
        self.name = name
        self.status = status
        self.dependencies = dependencies
        self.actions = actions

Task类表示一个工作流中的任务。它包含以下属性：

  • id：任务的唯一标识符。
  • name：任务的名称。
  • status：任务的状态，例如“pending”或“completed”。
  • dependencies：任务所依赖的其他任务的ID列表。
  • actions：任务执行时需要执行的动作（函数）列表。
  1. 定义WorkflowEngine类：
class WorkflowEngine:
    def __init__(self):
        self.tasks = {}
        self.execution_queue = []

WorkflowEngine类表示工作流引擎，它负责管理和执行任务。它包含以下属性：

  • tasks：一个字典，存储工作流中的所有任务，键是任务ID，值是任务对象。
  • execution_queue：一个列表，存储待执行的任务。
  1. add_task方法：
class WorkflowEngine:
    # ...
    def add_task(self, task):
        self.tasks[task.id] = task

add_task方法将任务添加到工作流引擎的tasks字典中。

  1. execute_task方法：
class WorkflowEngine:
    # ...

    def execute_task(self, task):
        print(f"Executing task {task.id}")
        # execute actions in task.actions
        for action in task.actions:
            action()
        task.status = 'completed'
        print(f"Task {task.id} completed\n")

execute_task方法负责执行单个任务。它首先打印一条消息表示任务正在执行，然后遍历任务的actions列表并执行每个动作。最后，将任务状态设置为“completed”并打印一条消息表示任务已完成。

  1. execute_workflow方法：
class WorkflowEngine:
    # ...
    def execute_workflow(self):
        for task in self.tasks.values():
            if not task.dependencies:
                self.execution_queue.append(task)

        while self.execution_queue:
            task = self.execution_queue.pop(0)
            if all(self.tasks[dep].status == 'completed' for dep in task.dependencies):
                self.execute_task(task)
                for dependent_task in self.tasks.values():
                    if task.id in dependent_task.dependencies:
                        dependent_task.dependencies.remove(task.id)
                        if not dependent_task.dependencies:
                            self.execution_queue.append(dependent_task)
            else:
                # 如果任务的依赖项尚未满足，将任务放回执行队列的末尾
                self.execution_queue.append(task)
                print(f"Task {task.id}'s dependencies:{task.dependencies} is not completed\n")
            time.sleep(0.1)  # 避免过度占用CPU资源

execute_workflow方法负责执行整个工作流。它首先将没有依赖项的任务添加到执行队列中。然后，当执行队列不为空时，从队列中取出一个任务并检查其所有依赖项是否已完成。如果所有依赖项都已完成，则执行任务，并从依赖于该任务的其他任务的依赖项列表中移除该任务。如果某个任务的依赖项列表为空，将其添加到执行队列中。这个过程会一直重复，直到执行队列为空。

  1. 创建任务和工作流引擎实例：
# 定义任务
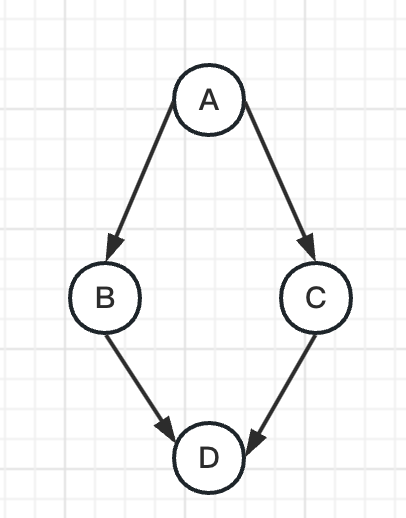
task_a = Task(id='A', name='Task A', status='pending', dependencies=[], actions=[])
task_b = Task(id='B', name='Task B', status='pending', dependencies=['A'], actions=[])
task_c = Task(id='C', name='Task C', status='pending', dependencies=['A'], actions=[])
task_d = Task(id='D', name='Task D', status='pending', dependencies=['B', 'C'], actions=[])

# 创建工作流引擎
workflow_engine = WorkflowEngine()

# 添加任务
workflow_engine.add_task(task_a)
workflow_engine.add_task(task_b)
workflow_engine.add_task(task_c)
workflow_engine.add_task(task_d)

# 执行工作流
workflow_engine.execute_workflow()

这部分代码创建了四个任务和一个工作流引擎实例。任务A没有依赖项，任务B和C依赖于任务A，任务D依赖于任务B和C。

最后添加任务并执行工作流。

image-20231031131533929

执行代码：

python dag.py

如果一切顺利，你会看到如下输出：

Executing task A
Task A completed

Executing task B
Task B completed

Executing task C
Task C completed

Executing task D
Task D completed
最后更新: 9/12/2024, 11:20:51 PM

← 4.2.2 开源Airflow DAG调度算法剖析 →